Compute the area of the region bounded by the curves $y - e x {(\log)}_{e} x a n d y = \frac{\log x}{e x}$

Video Solution

Text Solution

Verified by Experts

The given curves are
$y = e x \log_{e} x (1)$
$y = \frac{\log x}{e x} (2)$
The two curves intersect where $e x \log x = \frac{\log x}{e x}$
$\Rightarrow (e x - \frac{1}{e x}) \log x = 0 \Rightarrow x = \frac{1}{e} or x = 1$
$At x = 1 / e, y = - 1 (from (1))$
$At x = 1, y = 0 (from (1))$
So points of intersection are $(\frac{1}{e}, - 1) and (1, 0) .$

From the above information, the rough sketch of two curves is as shown in the figure and the shaded area is the required area.

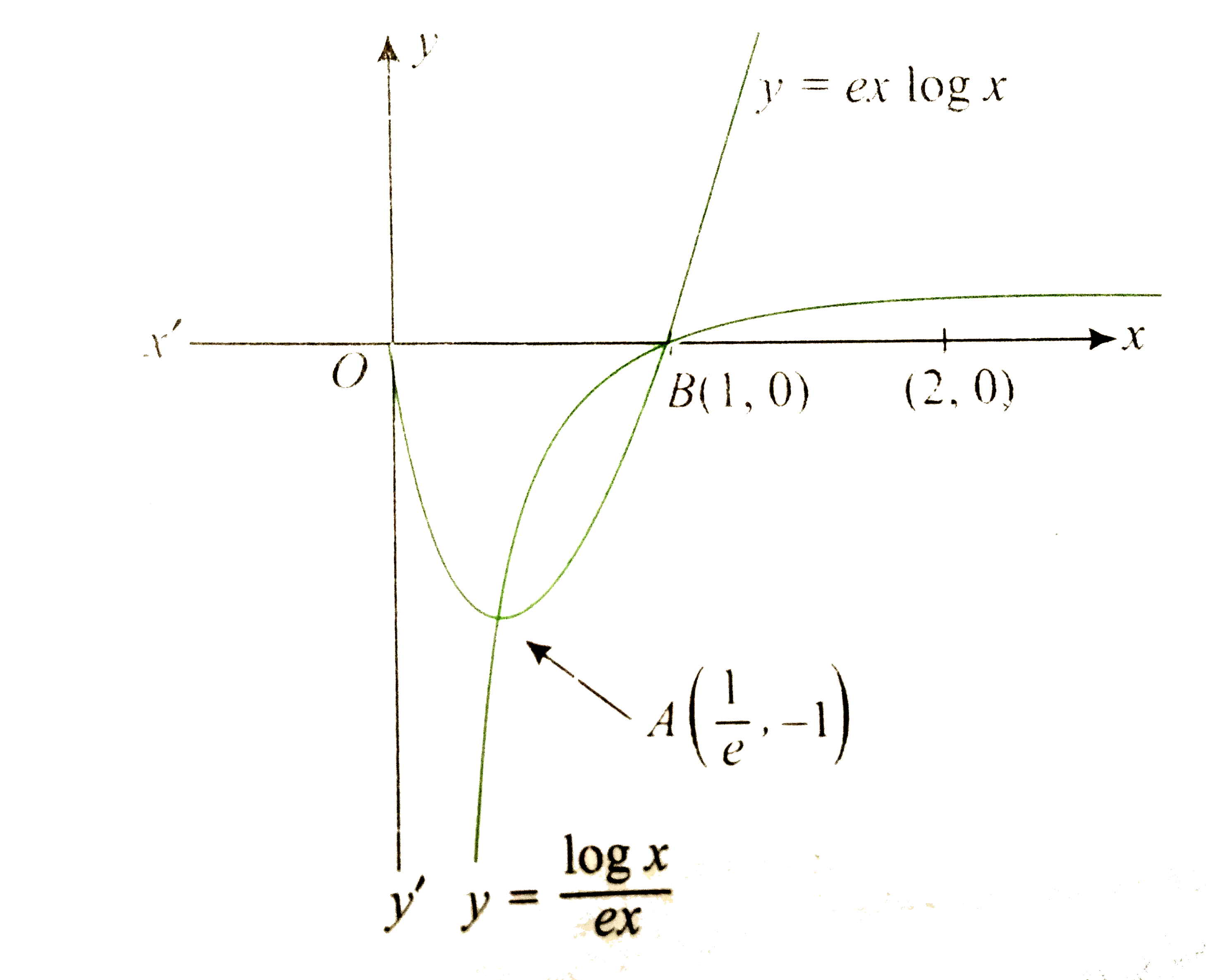
$∴$ Required area = Area of the shaded region
$= | \int_{1 / e}^{1} [e x \log x - \frac{\log x}{e x}] d x |$
$= | e {[\frac{x^{2}}{2} \log x - \frac{x^{2}}{4}]}_{1 / e}^{1} - \frac{1}{e} {[\frac{(\log x)}{2}]}_{1 / e}^{1} |$
$= | e [(- \frac{1}{4}) - (- \frac{1}{2 e^{2}} - \frac{1}{4 e^{2}})] - \frac{1}{e} [0 - \frac{1}{2}] |$
$| e [- \frac{1}{4} + \frac{3}{4 e^{3}}] + \frac{1}{2 e} |$
$= | \frac{5 - e^{2}}{4 e} | = \frac{e^{2} - 5}{4 e}$ sq. units.

Updated on:21/07/2023

Area of the region bounded by the curve $y = e^{x}$ and lines $x = 0$ and $y = e$ is
A $e - 1$
B $\int_{1}^{e} I n (e + 1 - y) d y$
C $e - \int_{0}^{1} e^{x} d x$
D $\int_{0}^{e} I n y d y$
The area (in sq units) of the region bounded by the curves $y = e^{x}$ , $y = {log}_{e}$ x and lines x = 1, x = 2 is
A ${(e - 1)}^{2}$
B $e^{2} - e + 1$
C $e^{2} - e + 1 - 2 {log}_{e} 2$
D $e^{2} + e - 2 {log}_{e} 2$