Compute the mode for the following frequency distribution:
To compute the mode for the given frequency distribution, we will follow these steps:
Step 1: Identify the Modal Class
The modal class is the class interval with the highest frequency.
- Given frequency distribution:
- 0 to 4: Frequency = 5
- 4 to 8: Frequency = 7
- 8 to 12: Frequency = 9
- 12 to 16: Frequency = 17 (highest frequency)
- 16 to 20: Frequency = 12
- 20 to 24: Frequency = 10
- 24 to 28: Frequency = 6
Modal Class: 12 to 16
Step 2: Assign Values
We will assign the following values based on the modal class:
- L (lower limit of modal class) = 12
- f1 (frequency of modal class) = 17
- f0 (frequency of the class before modal class) = 9 (frequency of 8 to 12)
- f2 (frequency of the class after modal class) = 12 (frequency of 16 to 20)
- h (class interval) = 16 - 12 = 4
Step 3: Use the Mode Formula
The formula for mode is given by:
Mode=L+f1−f02f1−f0−f2×h
Step 4: Substitute the Values
Substituting the values into the formula:
Mode=12+17−92×17−9−12×4
Step 5: Simplify the Expression
1. Calculate f1−f0:
17−9=8
2. Calculate 2f1−f0−f2:
2×17−9−12=34−9−12=13
3. Now substitute back:
Mode=12+813×4
4. Calculate 813×4:
3213≈2.46
5. Finally, add to L:
Mode=12+2.46≈14.46
Final Answer
The mode of the given frequency distribution is approximately 14.46.
---
The modal class is the class interval with the highest frequency.
- 0 to 4: Frequency = 5
- 4 to 8: Frequency = 7
- 8 to 12: Frequency = 9
- 12 to 16: Frequency = 17 (highest frequency)
- 16 to 20: Frequency = 12
- 20 to 24: Frequency = 10
- 24 to 28: Frequency = 6
We will assign the following values based on the modal class:
- L (lower limit of modal class) = 12
- f1 (frequency of modal class) = 17
- f0 (frequency of the class before modal class) = 9 (frequency of 8 to 12)
- f2 (frequency of the class after modal class) = 12 (frequency of 16 to 20)
- h (class interval) = 16 - 12 = 4
The formula for mode is given by:
Mode=L+f1−f02f1−f0−f2×h
Substituting the values into the formula:
Mode=12+17−92×17−9−12×4
1. Calculate f1−f0:
17−9=8
2. Calculate 2f1−f0−f2:
2×17−9−12=34−9−12=13
3. Now substitute back:
Mode=12+813×4
4. Calculate 813×4:
3213≈2.46
5. Finally, add to L:
Mode=12+2.46≈14.46
The mode of the given frequency distribution is approximately 14.46.
Topper's Solved these Questions
Similar Questions
Computer the mode for the following
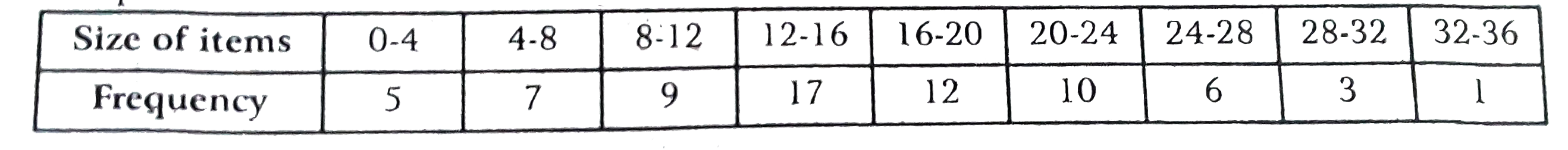 View Solution
View SolutionFind the mode of the following frequency distribution
 View Solution
View SolutionFind the mode of the following frequency distribution :
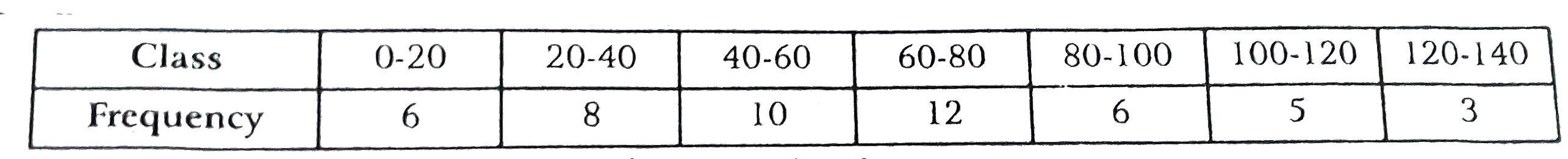 View Solution
View SolutionFind the median for the following frequency distribution:
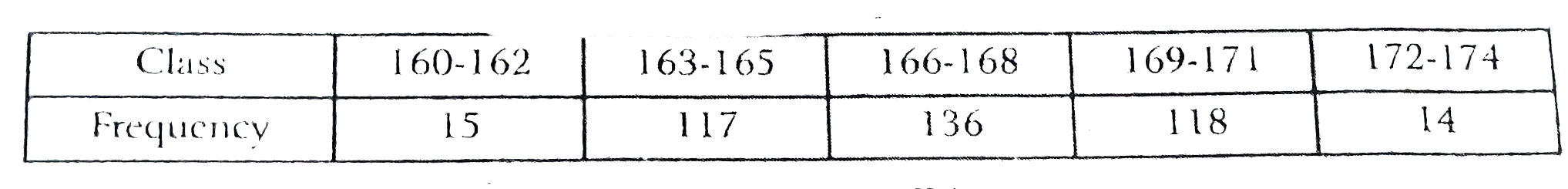 View Solution
View SolutionFind the mean for the following frequency distribution :
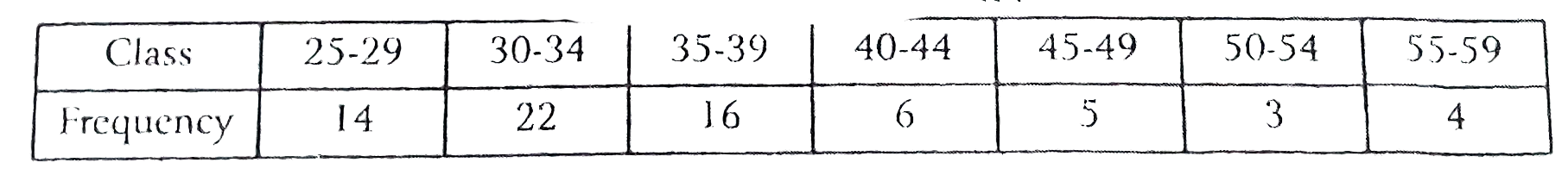 View Solution
View SolutionCompute the modal value for the following frequency distribution: x : 95 105 115 125 135 145 155 165 175 y : 4 2 18 22 21 19 10 3 2
View SolutionFind the mean deviation about the median for the following frequency distribution.
 View Solution
View SolutionCalculate the value of mode for the following frequency distribution :
 View Solution
View SolutionCalculate the mean deviation from the mean for the following frequency distributions.
 View Solution
View SolutionCalculate the mean deviation from the mean for the following frequency distributions.
 View Solution
View Solution

