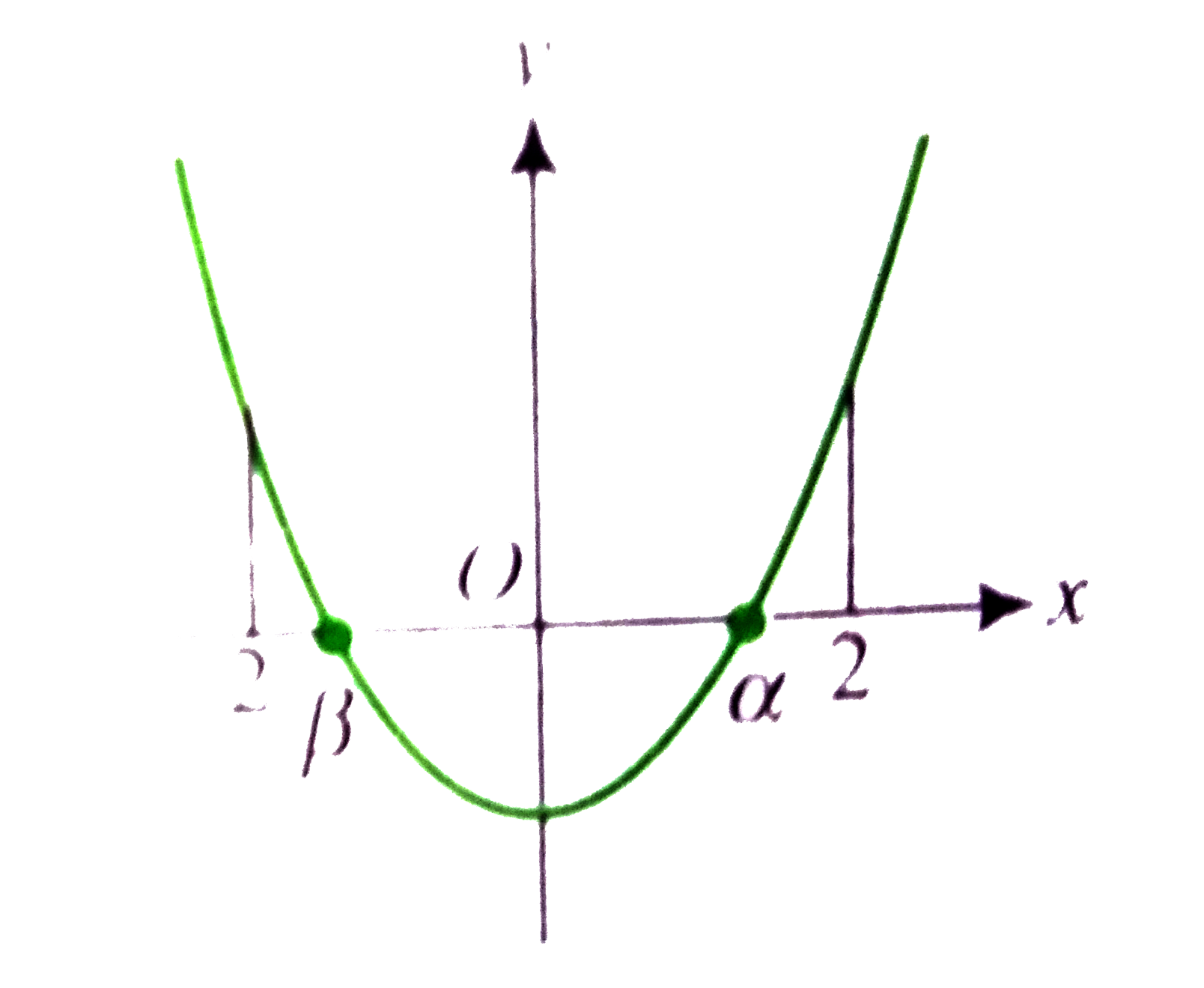
Consider a quadratic equation ax2+bx+c=0 having roots α,β. If 4a+2b+c>0,a−b+c<0and4a−2b+C>0 then |[α]+[β]| can be {where [] is greatest integer} Solution in Tamil
3
2
1
0
The correct Answer is:1,2,3
Form the given conditions we have following possible graph of y=f(x) Form the graph.
[α]=0or1,[β]=−2or−1
∴[α]+[β] can be 3,2,1
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Comprehension)
37 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matrix)
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single)
89 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
Similar Questions
Consider an unknow polynomial which divided by (x−3) and (x−4) leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by (x−3)(x−4).
If equations R(x)=x2+ax+1 has two distint real roots, then exhaustive values of a are.
View SolutionMatch the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionThe value of expression x4−8x3+18x2−8x+2 when x=2+√3
View Solutionabout to only mathematics
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionIf αandβ are roots of the quadratic equation ax2+bx+c=0 and a+b+c>0,a−b+c>0&c<0,then[α]+[β] is equal to (where [.] denotes the greatest integer function) 10 b. −3 c. −1 d. 0
View SolutionIf alpha and beta(alpha
View SolutionIf alpha,beta are the roots of the equation ax^(2)+bx+c=0 such that beta
View SolutionIf alpha and beta ( alpha
View SolutionConsider a quadratic equation ax^(2)+bx+c=0 having roots alpha,beta. If 4a+2b+c>0,a-b+c then [[alpha]+[beta]| can be { where [] is greatest integer }
View SolutionLet αandβ be the roots of the quadratic equation ax2+bx+c=0,c≠0, then form the quadratic equation whose roots are 1−ααand1−ββ.
View SolutionLet a, b, c ∈ R and α,β are the real roots of the equation ax2 + bx + c = 0 and if a + b + c < 0, a – b + c < 0 and c > 0 then [α]+[β] is equal to (where [.] denotes the greatest integer function.)
View SolutionIf α,β are the roots of ax2+bx+c=0, αβ=3 and a, b, c are in A.P., then α+β =
View SolutionConsider a quadratic equation ax2+bx+c=0 having roots α,β. If 4a+2b+c>0,a−b+c<0and4a−2b+C>0 then |[α]+[β]| can be {where [] is greatest integer}
View Solutionα,β are roots of quadratic equation ax2+bx+c=0. Then (α+β)=______ a)−ba b)ba c)−ca d)ca
View Solution
