Consider a semicircle of radius 1 unit constructed on the diameter AB, and let O be its centre. Let C be a point on AO such that AC : CO = 2:1. Draw CD perpendicular to AO with D on the semicircle. Draw OE perpendicular to AD with E on AD. Let OE and CD intersects at H. Then DH equals
1√5
1√3
1√2
√5−12
The correct Answer is:c
E is mid point of AD.
thetacos2θ=13⇒cos2θ−1=13
cos2θ=23
cosθ√2√3
sinθ=√1−23=1√3
ED1=1√3
DH=EDsecθ
1√3×√3√2
1√2
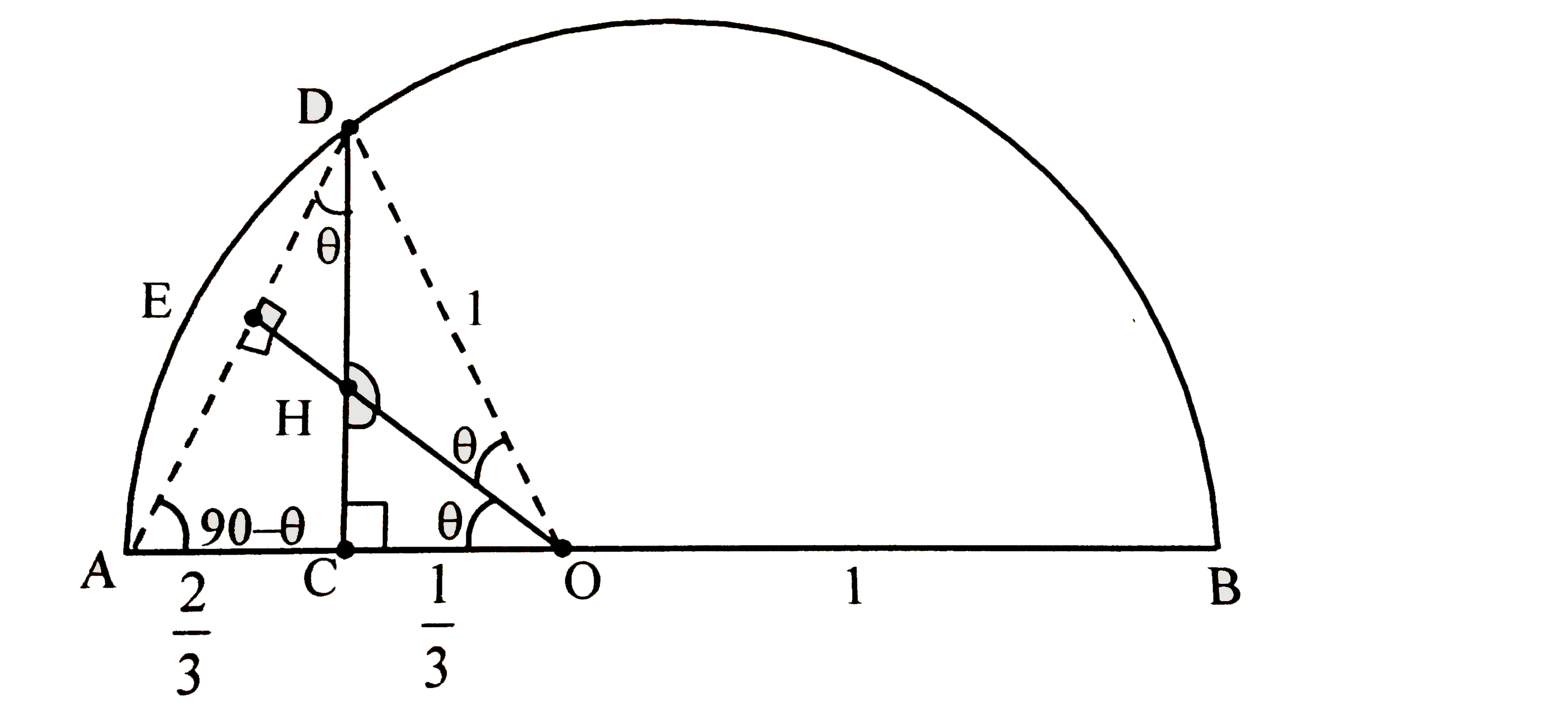
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Mathematics
45 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - exercise
18 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics
15 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Draw a line segment AB=6 cm. Take a point C on AB such that AC=2.5 cm. Draw CD perpendicular to AB.
View SolutionLet AB be a line segment with midpoint C, and D be the midpoint of AC. Let C1 be the circle with diameter AB and C2 be the circle with diameter AC. Let E be a point on C1 such that EC is perpendicular to AB. Let f be a point on C2such that DF is perpendicular to AB. Then, the value of sin∠FEC is
View Solution
Knowledge Check
Suppose AB is a diameter of a circle, whose centre is at O and C be any point on the circle. If CD is perpendicular to AB and CD = 12 cm, AD = 16 cm, then BD is equal to
A10 cmB12 cmC8 cmD9 cmThe middle point of A (1, 2) and B (x, Y) is C (2, 4). If BD is perpendicular to AB such that CD=3 unit, then what is the length BD ?
A2√2 unitB2 unitC3 unitD3√2 unitThe middle point of A (1, 2) and B (x, y) is C (2, 4). If BD is perpendicular to AB such that CD = 3 unit, then what is the length BD ?
A2√2 unitB2unitC3 unitD3√2 unit
AB is a straight line, C and D are points on the same side of AB such that AC is perpendicular to AB and DB is perpendicular to AB. Let AD and BC meet at E.
What is AEAD+DEBC equal to ?
View SolutionDraw a circle of radius 3 cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
View SolutionIn the given fig, AB is the diameter of the circle with centre O. The point C, D and E are on the circle such that AC = CD = DE = EB. Find ∠EBA.
View SolutionABC is a triangle. Let D, E denote the mid points of BC, CA respectively. Let AD and BE intersect at G. Let O be a point on AD such that AO:OD=2:7.
Assertion (A): AO=(2GD)/3
Reason (R) : OD=(2AG)/3
View SolutionLet ABC be an equilateral triangle. If the side BC is produced to the point D so that BC = 2CD, then AD2 is equal to
View Solution
