Consider a triangle ABC, where x,y,z are the length of perpendicular drawn from the vertices of the triangle to the opposite sides a,b, c respectively. Let the letters R,r,S,Δ denote the circumradius, inradius semi-perimeter and area of the triangle respectively.
The valur of csinB+bsinCx+asinC+csinAy+bsinA+asinBz is equal to Solution in Punjabi
Rr
SR
2
6
The correct Answer is:D
Step by step video & image solution for Consider a triangle ABC, where x,y,z are the length of perpendicular drawn from the vertices of the triangle to the opposite sides a,b, c respectively. Let the letters R,r,S,Delta denote the circumradius, inradius semi-perimeter and area of the triangle respectively. The valur of (c sin B+b sin C)/(x)+ (a sin C +c sin A)/(y)+(b sin A+a sin B)/(z) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Single Integer Answer Type Questions)
16 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
15 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statement of Colume I with values of Column II.
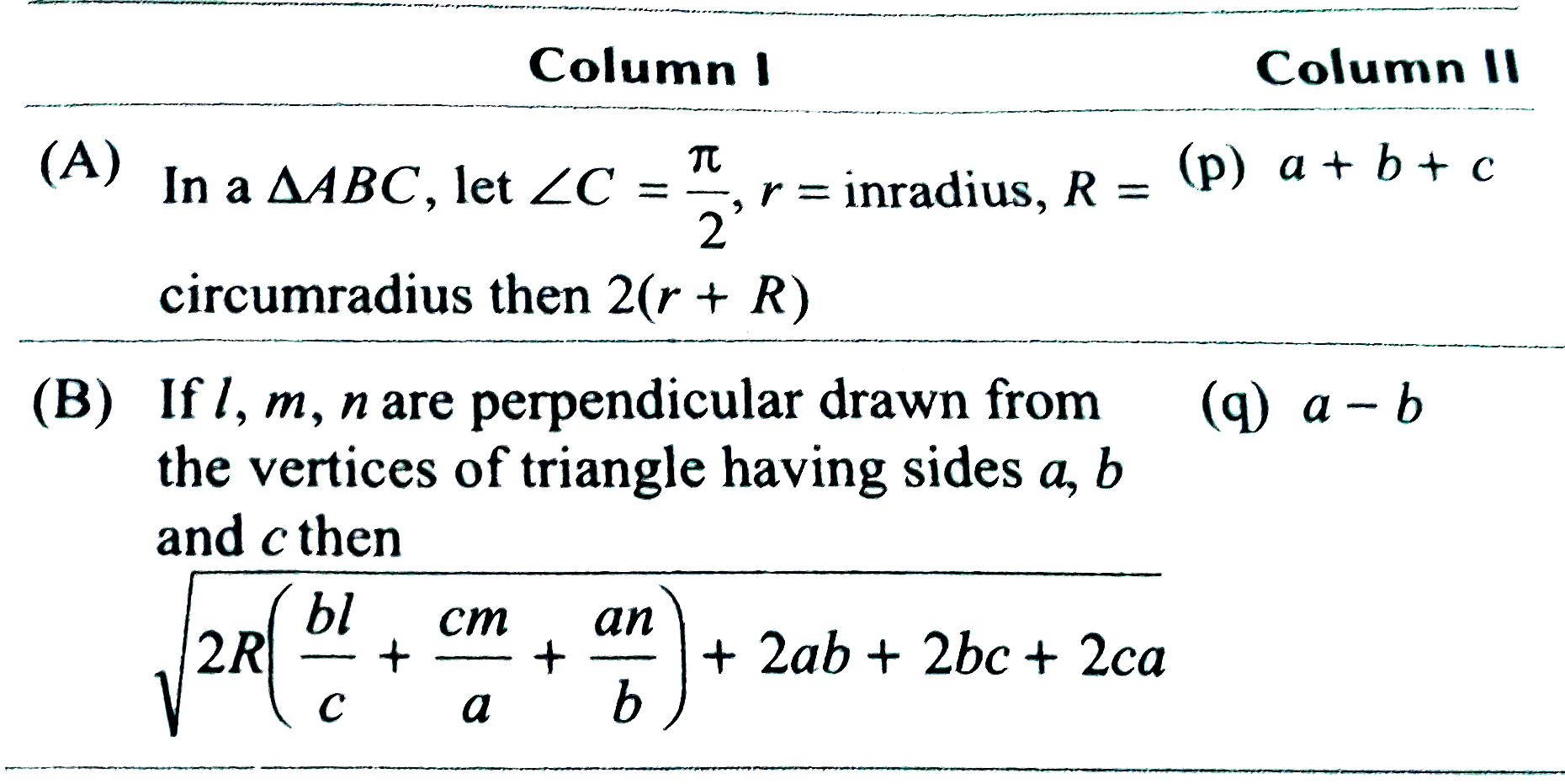
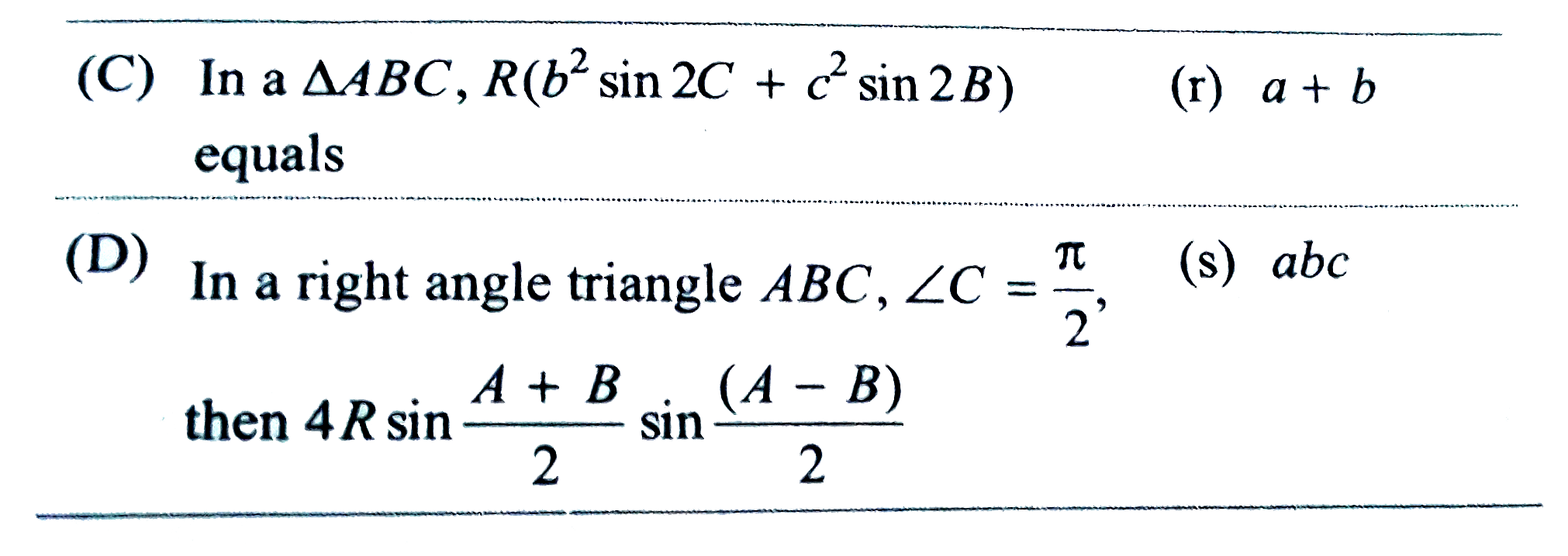
View SolutionIf in ΔABC,∠C=π8,a=√2andb=√2+√2 then find the measure of angle A (in degree).
View SolutionIn a triangle ABC,a3+b3+c3=c2(a+b+c) (All symbol used have usual meaning in a triangle.) Statement-1: The value of ∠C=60∘. Statement-2: ΔABC must be equilateral.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf in a Delta ABC, the altitudes from the vertices A,B,C on opposite sides are in H.P.then sin Asin B, sin C are in
View SolutionIf A,B,C are the angles of a triangle,the system of equations,(sin A)x+y+z=cos A,x+(sin B)y+z=cos B,x+y+(sin C)z=1-cos C has
View SolutionIn Delta ABC,a,b,c are the opposite sides of the angles A,B and C respectively,then prove (sin B)/(sin(B+C))=(b)/(a)
View SolutionConsider a triangle ABC, where c,y,z are the length of perpendicular drawn from the vertices of the triangle to the opposite sides a,b, c respectively. Let the letters R,rS,Δ denote the circumradius, inradius semi-perimeter and area of the triangle respectively.
If bxc+cya+azb=a2+b2+c2k, then the value of k is
View SolutionConsider a triangle ABC, where c,y,z are the length of perpendicular drawn from the vertices of the triangle to the opposite sides a,b, c respectively. Let the letters R,rS,Δ denote the circumradius, inradius semi-perimeter and area of the triangle respectively.
If cotA+cotB+cotC=k(1x2+1y2+1z2), then the value of k is
View SolutionUsing vectors , prove that in a triangle ABC
asinA=bsinB=csinC
where a,b,c are lengths of the ideas opposite to the angles A,B,C of triangle ABC respectively .
View SolutionΔABC में सिद्ध कीजिए कि -
Δ=b2−c22⋅sinBsinCsin(B−C)
View SolutionIf in a triangle ABC, bsinB=csinC, then the triangle is-
View Solutionयदि ΔABC में शीर्षों A ,B तथा C से सम्मुख भुजाओं पर खींचे गए शीर्ष लम्ब हरात्मक श्रेणी में हों,sinA,sinB,sinC है|
View Solutionकिसी त्रिभुज ABC में सिद्ध कीजिए - sinAa=sinB+sinCb+c=sinB−sinCb−c.
View SolutionIn ΔABC,if(sinA+sinB+sinC)(sinA+sinB−sinC)=3sinAsinB, then
View Solution
