Consider four circles ${(x \pm 1)}^{2} + {(y \pm 1)}^{2} = 1$ . Find the equation of the smaller circle touching these four circles.

A

$(\sqrt{2} - 1) a$

B

$(\sqrt{2} + 1) a$

C

$(2 + \sqrt{2} a)$

D

$(2 - \sqrt{2}) a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

It is evident from the figure that the smallest circle touching all the circles has radius equal to
$O P = O C_{1} - C_{1} P = \sqrt{2} a - a = (\sqrt{2} - 1) a$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider four circles ${(x \pm 1)}^{2} + {(y \pm 1)}^{2} = 1$ . Find the equation of larger circle touching these four circles.
A $x^{2} + y^{2} = {(\sqrt{2} + 1)}^{2}$
B $x^{2} + y^{2} = {(\sqrt{2} - 1)}^{2}$
C $x^{2} + y^{2} = {(2 - \sqrt{2})}^{2}$
Dnone of these
Question 2 - Select One
There are four circles each of radius 1 unit touching both the axis. The equation of the smaller circle touching all these circle is
A $x^{2} + y^{2} = 2$
B $x^{2} + y^{2} = {(\sqrt{2} - 1)}^{2}$
C $x^{2} + y^{2} = 4$
D $x^{2} + y^{2} = 1$
Question 3 - Select One
In the figure below, the radius of the bigger circle is $(\sqrt{2} + 1)$ cm and the radius of all the smaller circles are equal. Each of the smaller circles touches two of the other three smaller circles and the larger circle as shown. Find the area (in cm2) of the shaded portion.

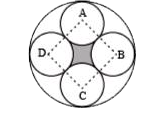A $2 - \frac{π}{2}$
B1
C $π / 4$
DCannot to determined

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile