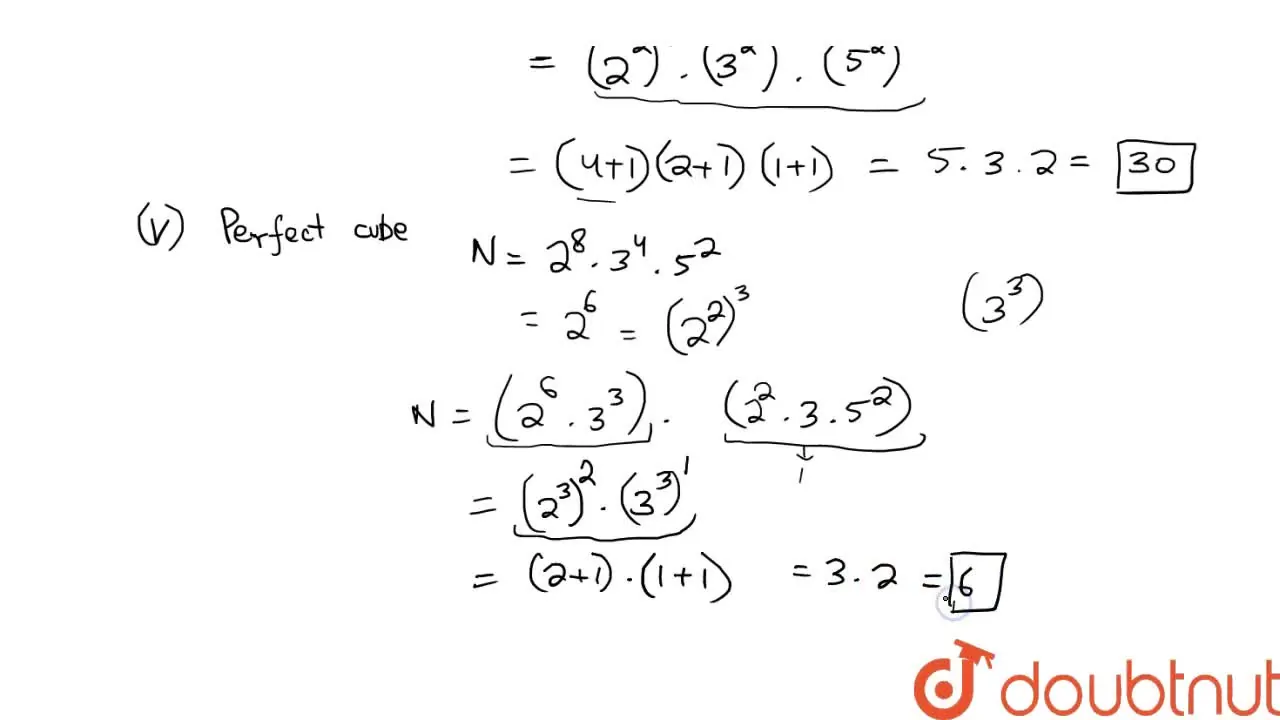Consider and give the answers of the following questions .
(i) Find the total number of divisible of N .
(ii) Find the total number of divisors divisible by 24
(iii) Find the total number of divisors divisible by 5.
(iv) Find the total number of divisors which are perfect square.
(v) Find the number of divisors which are perfect cube.
(i) Total divisors =(8+1)(4+1)(2+1)=135
(ii) N=(24)
Total divisors divisible by 24=(6+1)(3+1) (2+1)=84
(iii) , total divisors divisible by 5 is (8+1)(4+1)(1+1)=90
(iv) , number of perfect square divisors =(4+1)(2+1)(1+1)=30
(v) , number of perfect cube divisors =(2+1)(1+1)=6
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself65videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )51videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions3videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)12videos
PRINCIPLE OF MATHEMATICAL
Similar Questions
Find the largest number of 2 digits which is a perfect square.
Find the largest number of 3 digits which is a perfect square.View SolutionFind the total number of different divisors of 2525
View SolutionIf N = 10800, find the(i) the number of divisors of the form 4m +2,(ii) the number of divisors which are multiple of 10(iii) the number of divisors which are multiple of 15.
View SolutionFind the 5 - digit number which is a perfect square.
View SolutionThe total number of 6-digit numbers in which the sum of the digits is divisible by 5, is
View SolutionFind the least square number which is divisible by 3, 5, 6, and 9.
View SolutionThe number of divisors of 12780 which are of the form (4k+2),k∈W is
View SolutionIf n=10800, then find the
a. total number of divisors of n.
(b) The numberof even divisors.
(c) The number of divisors of the form 4m+2.
(d) The number of divisors which are multiples of 15.View SolutionConsider N=33⋅43⋅63, then the number of divisors of N, which are perfect cubes, is
View SolutionFind the smallest perfect square divisible by 3, 4, 5 and 6.
View Solution