Consider point P(x, y) in first quadrant. Its reflection about x-axis is Q(x1,y1). So, x1=x and y(1)=−y.
This may be written as : {x1=1.x+0.yy1=0.x+(−1)y
This system of equations can be put in the matrix as :
[x1y1]=[100−1][xy]
Here, matrix [100−1] is the matrix of reflection about x-axis. Then find the matrix of
(i) reflection about y-axis
(ii) reflection about the line y=x
(iii) reflection about origin
(iv) reflection about line y=(tanθ)x
(i) Reflection of (x, y) about y-axis is (x1,y1)≡(−x,y).
∴x1=(−1)x+0y
and y1=0x+y
∴[x1y1]=[−1001][xy]
(ii) Reflection of (x, y) about the line y=x is (x1,y1)≡(y,x).
∴x1=0x+y
y1=x+0y
∴[x1y1]=[0110][xy]
(iii) Reflection of (x, y) about origin is (x1,y1)≡(−x,−y).
∴x1=−x+0y
y1=0x−y
∴[x1y1]=[−100−1][xy]
(iv) Reflecton in line t=xtanθ or (sinθ)x−(cosθ)y=0:
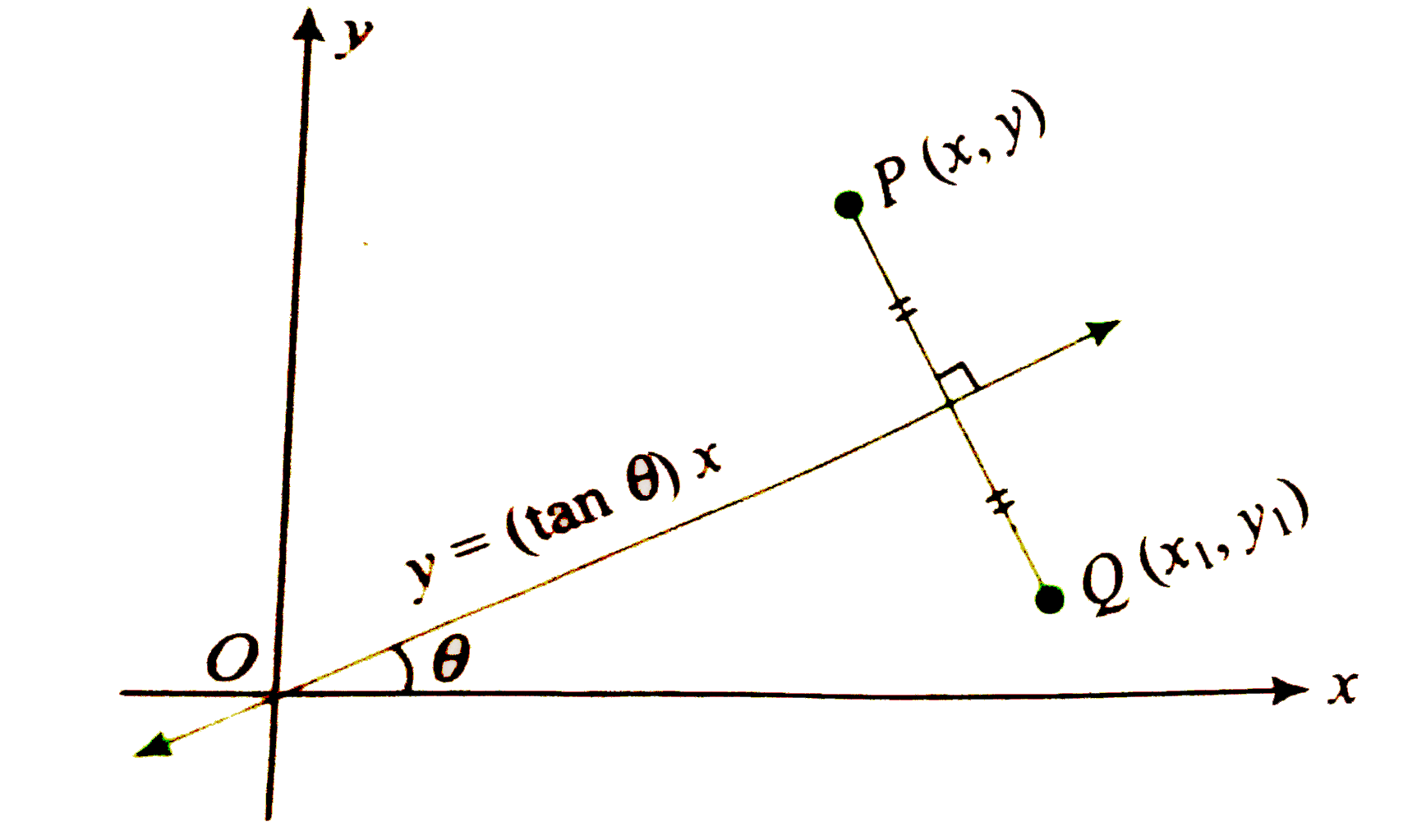
We kanow that
x1−xsinθ=y1−y−cosθ=−2((sinθ)x−(cosθ)y)sin2θ+cos2θ
∴x1=(1−2sin2θ)x+(2sinθcosθ)y
or x1=(cos2θ)x+(sin2θ)y
y1=(2sinθcosθ)x+(1−2cos2θ)y
or y1=(sin2θ)x−(cos2θ)y
Thus, [x1y1]=[cos2θsin2θsin2θ−cos2θ][xy]
By putting θ=0,π/2,π/4, we can get the reflection matrices x-axis, y-axis and the line y=x, respectively.
Topper's Solved these Questions
- MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise 13.1
5 Videos
- MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise 13.2
6 Videos
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year
10 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
Similar Questions
Consider point P(x, y) in first quadrant. Its reflection about x-axis is Q(x1,y1). So, x1=x and y(1)=−y.
This may be written as : {x1=1.x+0.yy1=0.x+(−1)y
This system of equations can be put in the matrix as :
[x1y1]=[100−1][xy]
Here, matrix [100−1] is the matrix of reflection about x-axis. Then find the matrix of reflection about the line y=x.
View SolutionReflection of y2=x about y-axis is
View Solution
Knowledge Check
The position of reflection of the point (4,1) about the line y=x -1 is
A1,2B3,4C−1,0D2,3
Reflection of y2=x about y-axis is
View SolutionThe matrix [0110] is the matrix of reflection in the line (A) x−y=0 (B) x+y=0 (C) x−y=1(D)x+y=1
View SolutionThe matrix of the transformation reflection in the line x+y=0 is (A) [−100−1] (B) [100−1] (C) [0110] (D) [0−1−10]
View SolutionThe matrix of the transformation reflection in the line x+y=0 is (A) [−100−1] (B) [100−1] (C) [0110] (D) [0−1−10]
View SolutionIf the reflection of 2x+y-1=0 about the line x+y+3=0, is ax+by+10=0 then b is equal to
View SolutionUse (xy)=(−1001)(xy) to find the coordinates of images of the following pointes when reflected on the y-axis
(1,1)
View SolutionUse (xy)=(−1001)(xy) to find the coordinates of images of the following pointes when reflected on the y-axis
(2,3)
View Solution
