Consider point P(x, y) in first quadrant. Its reflection about x-axis is $Q (x_{1}, y_{1})$ . So, $x_{1} = x$ and $y (1) = - y$ .
This may be written as : ${\begin{matrix} x_{1} = 1 . x + 0 . y \\ y_{1} = 0 . x + (- 1) y \end{matrix}$
This system of equations can be put in the matrix as :
$[\begin{matrix} x_{1} \\ y_{1} \end{matrix}] = [\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
Here, matrix $[\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}]$ is the matrix of reflection about x-axis. Then find the matrix of reflection about the line $y = x$ .

Video Solution

Text Solution

Verified by Experts

(i) Reflection of (x, y) about y-axis is $(x_{1}, y_{1}) \equiv (- x, y)$ .
$∴ x_{1} = (- 1) x + 0 y$
and $y_{1} = 0 x + y$
$∴ [\begin{matrix} x_{1} \\ y_{1} \end{matrix}] = [\begin{matrix} - 1 & 0 \\ 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
(ii) Reflection of (x, y) about the line $y = x$ is $(x_{1}, y_{1}) \equiv (y, x)$ .
$∴ x_{1} = 0 x + y$
$y_{1} = x + 0 y$
$∴ [\begin{matrix} x_{1} \\ y_{1} \end{matrix}] = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
(iii) Reflection of (x, y) about origin is $(x_{1}, y_{1}) \equiv (- x, - y)$ .
$∴ x_{1} = - x + 0 y$
$y_{1} = 0 x - y$
$∴ [\begin{matrix} x_{1} \\ y_{1} \end{matrix}] = [\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
(iv) Reflecton in line $t = x \tan θ$ or $(\sin θ) x - (\cos θ) y = 0$ :

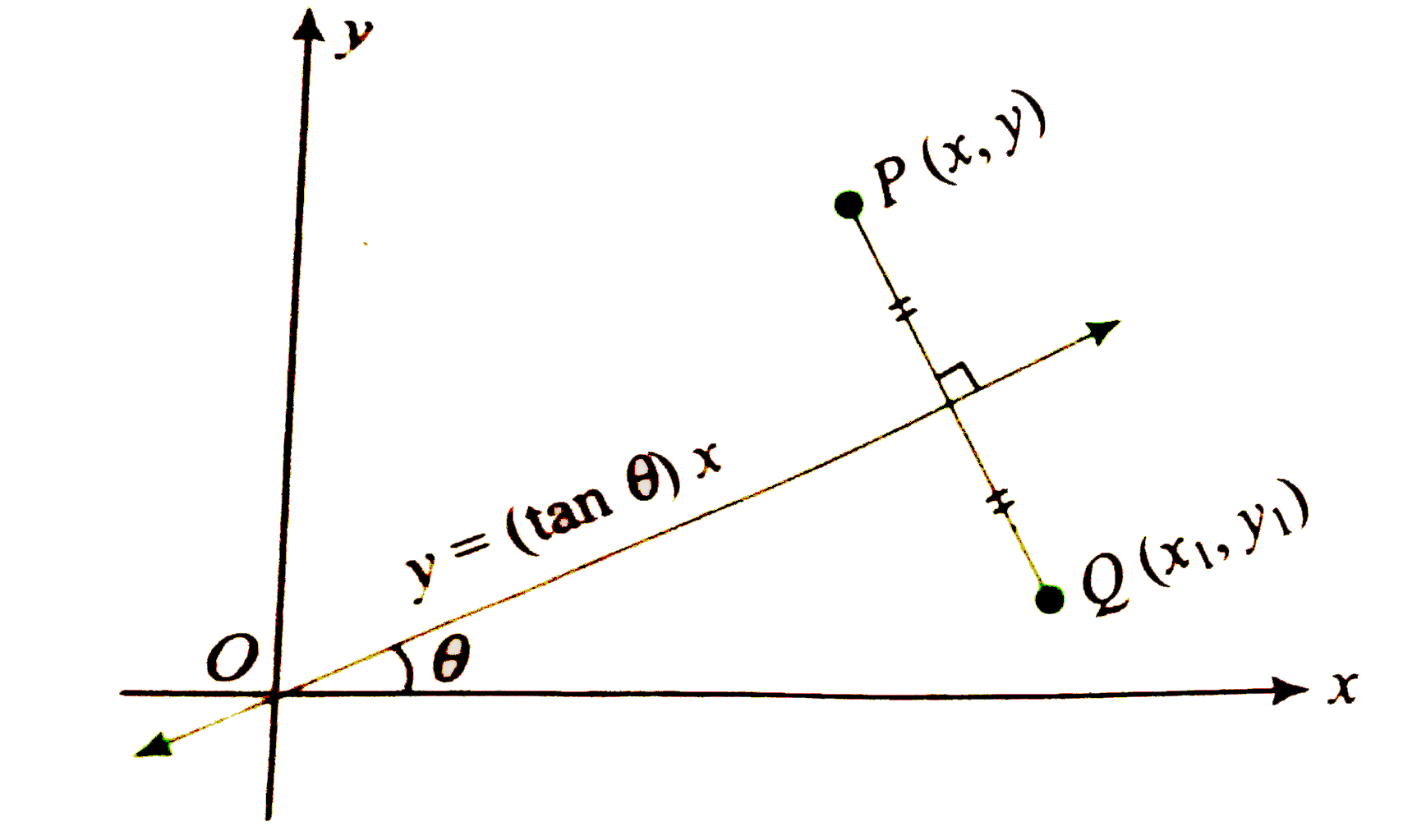
We kanow that
$\frac{x_{1} - x}{\sin θ} = \frac{y_{1} - y}{- \cos θ} = \frac{- 2 ((\sin θ) x - (\cos θ) y)}{\sin^{2} θ + \cos^{2} θ}$
$∴ x_{1} = (1 - 2 \sin^{2} θ) x + (2 \sin θ \cos θ) y$
or $x_{1} = (\cos 2 θ) x + (\sin 2 θ) y$
$y_{1} = (2 \sin θ \cos θ) x + (1 - 2 \cos^{2} θ) y$
or $y_{1} = (\sin 2 θ) x - (\cos 2 θ) y$
Thus, $[\begin{matrix} x_{1} \\ y_{1} \end{matrix}] = [\begin{matrix} \cos 2 θ & \sin 2 θ \\ \sin 2 θ & - \cos 2 θ \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
By putting $θ = 0, π / 2, π / 4$ , we can get the reflection matrices x-axis, y-axis and the line y=x, respectively.

Updated on:21/07/2023

Equations of diagonals of the square formed by the lines $x = 0, y = 0, x = 1$ and $y = 1$ are
A $y = x, x + y = 2$
B $2 y = x, y + x = \frac{1}{3}$
C $y = x, y + x = 1$
D $y = 2 x, y + 2 x = 1$