Consider the following statements concerning a ΔABC
(i) The sides a,b,c and area of triangle are rational.
(ii) a,tanB2,tanC2
(iii) a,sinAsinB,sinC are rational .
Prove that (i)⇒(ii)⇒(iii)⇒(i) Solution in Punjabi
The correct Answer is:Hence (iii)⇒(i).
Step by step video & image solution for Consider the following statements concerning a DeltaABC (i) The sides a,b,c and area of triangle are rational. (ii) a, "tan"(B)/(2),"tan"(C)/(2) (iii) a, sin A sin B, sin C are rational . Prove that (i) rArr(ii) rArr(iii)rArr(i) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
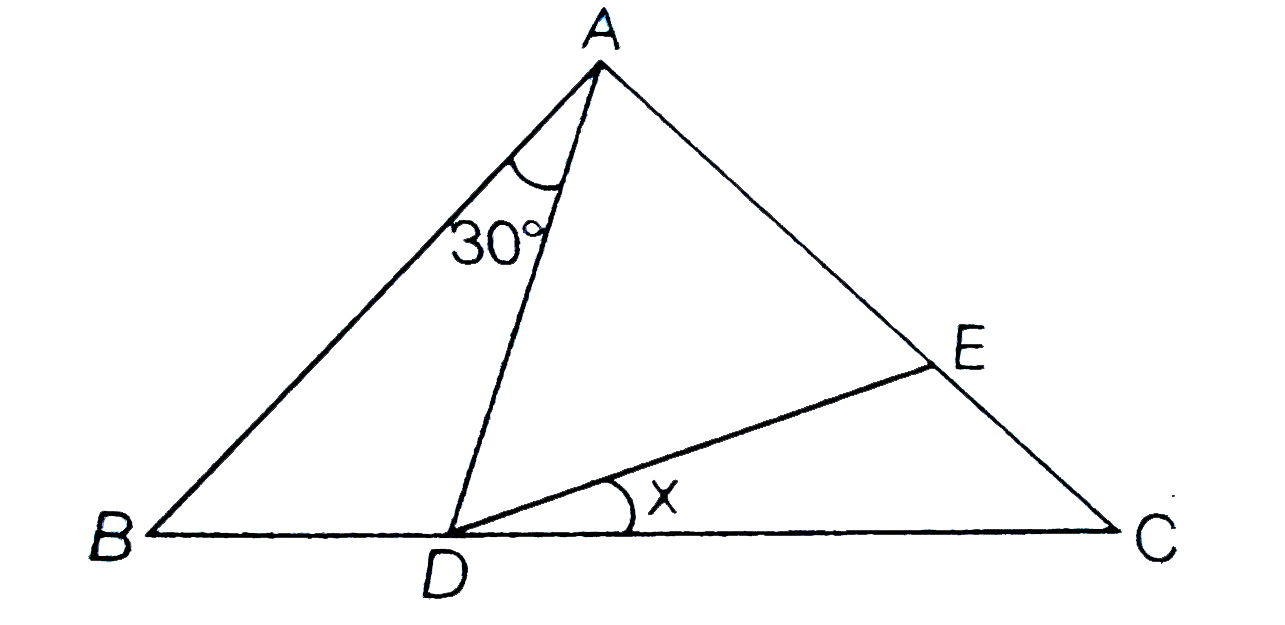
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionComplete the following reactions: a. H−C(A)≡C−H1mol−−−−→NaNH2(B)CH3Br−−−→(C)

g. H−C≡C(A)−H1mol−−−−→NaNH2(B)Br(CH2)8Br−−−−−−−−→(C)

View SolutionIn triangle ABC prove that
(i) sinA=sin(B+C) (ii)sin2A=−sin(2B+2C)
(iii)cosA=−cos(A+B) (iv)tan(A+B2)=cot.C2
View SolutionConsider the following statements concerning a ΔABc (i) The sides a,b,c and area of triangle are rational. (ii) a,tanB2,tanC2 are rational (iii) a,sinAsinB,sinC are rational . Prove that (i)⇒(ii)⇒(iii)⇒(i)
View Solution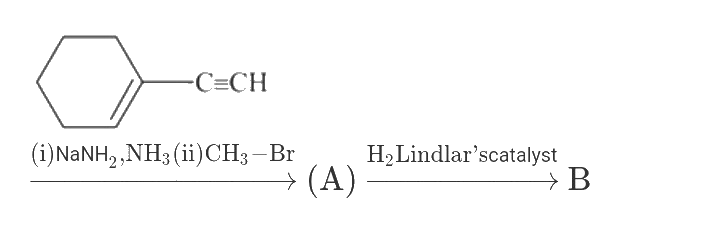
(i)NaNH2,NH3(ii)CH3−Br−−−−−−−−−−−−−−−−−−−→(A)(H2 Lindlar'scatalyst)−−−−−−−−−−−−−−→B
View SolutionIn the reaction CH3−C≡C−H(i)NaNH2/NH3(l)−−−−−−−−−−−−−→(A)CH3−CH2−CH2−Br−−−−−−−−−−−−−→(B) The product B is
View SolutionIn a △ABC, the correct formulae, among the following are
I r=4Rsin(A)2sin(B)2sin(C)2
II r1=(s−a)tan(A)2
III r3=△(s−c)
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View SolutionIn the reaction :
CH3−C≡C−H(i)NaNH2/NH3(I)−−−−−−−−−−−−−→(A)CH3−CH2−CH2−Br−−−−−−−−−−−−−→(B)
the product (B) is :
View SolutionIn any triangle ABC,prove that:
(i) sin(A+B)=sinC
(ii)cos(A+B2)=sinC2
(iii)tan(B+C−A2)=cotA.
View SolutionProve in any △ ABC that
(i)tanCtanA=b2+c2−a2a2+b2−c2
b2sin2C+c2sin2B=2bcsinA.
View SolutionIf A+B+C=180∘ prove that:
(i) sin(B+C−A)+sin(C+A−B)
+sin(A+B−C)=4sinAsinBsinC
(ii) cos(−A+B+C)+cos(A−B+C)
+cos(A+B−C)=1+4cosAcosBcosC
(iii) tan(B+C−A)+tan(C+A−B)
+tan(A+B−C)
=tan(B+C−A)tan(C+A−B)tan(A+B−C)
View SolutionIn triangle ABC prove that
(i) sinA=sin(B+C) (ii)sin2A=−sin(2B+2C)
(iii)cosA=−cos(A+B) (iv)tan(A+B2)=cot.C2
View Solution
