Consider the function f(x)=x2+bx+c, where D=b2−4c>0, then match the follwoing columns.

Text Solution
The graph of following data is as given below
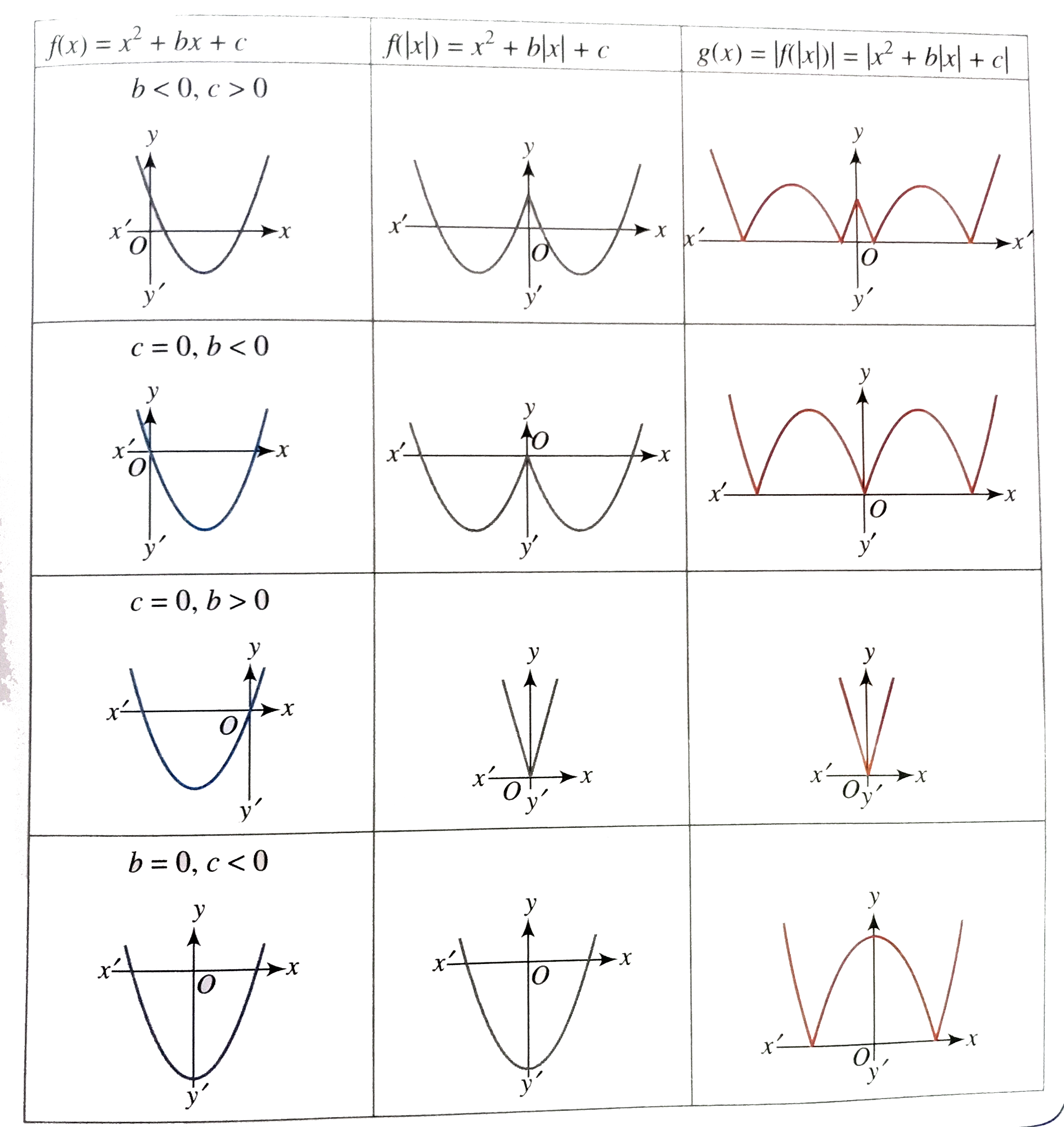
|
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
Similar Questions
Knowledge Check
Consider that f(x)=ax2+bx+c,D=b2−4ac , then which of the following is not true ?
AIf a>0 then minimum value of f(x) is −D4aBIf a<0, then maximum value of f(x) is −D4aCif a>0,D<0, then f(x)>0 for all x ∈ RDIf a>0,D>0 , then f(x)>0 for alll x∈RConsider the function f(x)=(ax+1bx+2)x, where a,b>0, the limx→∞f(x) is
Aexists for all values of a and bBzer for a<bCnon existent for a>bDe−(1/a) or e−(1/b) if a=bConsider the function f(x)=(1x)2x2, where x>0 .
The minimum value of the function is:AeBe2eCe1xD1e
For the quadratic polynomial f(x)=ax2+bx+c where a,b,c∈Randa≥0. Match the condition column-1 with its no. of points of non-derivablity of y=|f(|x|)| in column-II
View SolutionConsider the quadratic function f(x)=ax2+bx+c where a,b,c∈R and a≠0, such that f(x)=f(2−x) for all real number x. The sum of the roots of f(x) is
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionThe function f(x)=x2+bx+c, where b and c are real constants, describes
View Solution
