Consider that f(x)=ax2+bx+c,D=b2−4ac , then which of the following is not true ?
If a>0 then minimum value of f(x) is −D4a
If a<0, then maximum value of f(x) is −D4a
if a>0,D<0, then f(x)>0 for all x ∈ R
If a>0,D>0 , then f(x)>0 for alll x∈R
The correct Answer is:D
To solve the problem, we need to analyze the properties of the quadratic function f(x)=ax2+bx+c and its discriminant D=b2−4ac. We will evaluate the statements regarding the function and identify which one is not true.
1. Understanding the Quadratic Function:
The function f(x)=ax2+bx+c is a quadratic function. The shape of the graph (parabola) depends on the coefficient a.
2. Discriminant Analysis:
The discriminant D=b2−4ac helps us determine the nature of the roots of the quadratic equation:
- If D>0: The quadratic has two distinct real roots.
- If D=0: The quadratic has exactly one real root (a repeated root).
- If D<0: The quadratic has no real roots (the parabola does not intersect the x-axis).
3. Case 1: a>0:
- The parabola opens upwards.
- If D<0, the vertex of the parabola is the minimum point, and the function value f(x) is always greater than 0 for all real x.
4. Case 2: a<0:
- The parabola opens downwards.
- If D<0, the vertex is the maximum point, and the function value f(x) is always less than 0 for all real x.
5. Evaluating the Statements:
- Statement 1: When a>0 and D<0, f(x) is always positive. (True)
- Statement 2: When a<0 and D<0, f(x) is always negative. (True)
- Statement 3: When a>0 and D>0, the function has two real roots and will cross the x-axis. (True)
- Statement 4: When a>0 and D>0, the function value f(x) can be less than 0 between the roots. (False)
6. Conclusion:
The statement that is not true is Statement 4. When a>0 and D>0, the function will cross the x-axis, and there will be intervals where f(x) is indeed less than 0, specifically between the two roots.
Final Answer:
The statement that is not true is Statement 4.
The function f(x)=ax2+bx+c is a quadratic function. The shape of the graph (parabola) depends on the coefficient a.
The discriminant D=b2−4ac helps us determine the nature of the roots of the quadratic equation:
- If D>0: The quadratic has two distinct real roots.
- If D=0: The quadratic has exactly one real root (a repeated root).
- If D<0: The quadratic has no real roots (the parabola does not intersect the x-axis).
- The parabola opens upwards.
- If D<0, the vertex of the parabola is the minimum point, and the function value f(x) is always greater than 0 for all real x.
- The parabola opens downwards.
- If D<0, the vertex is the maximum point, and the function value f(x) is always less than 0 for all real x.
- Statement 1: When a>0 and D<0, f(x) is always positive. (True)
- Statement 2: When a<0 and D<0, f(x) is always negative. (True)
- Statement 3: When a>0 and D>0, the function has two real roots and will cross the x-axis. (True)
- Statement 4: When a>0 and D>0, the function value f(x) can be less than 0 between the roots. (False)
The statement that is not true is Statement 4. When a>0 and D>0, the function will cross the x-axis, and there will be intervals where f(x) is indeed less than 0, specifically between the two roots.
The statement that is not true is Statement 4.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -C) (objective Type Questions ( more thena one options are correct )
35 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -D) Linked comprehension Type Questions
14 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -A) (objective Type Questions ( one option is correct)
47 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)
4 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
16 Videos
Similar Questions
Knowledge Check
If in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
A B
B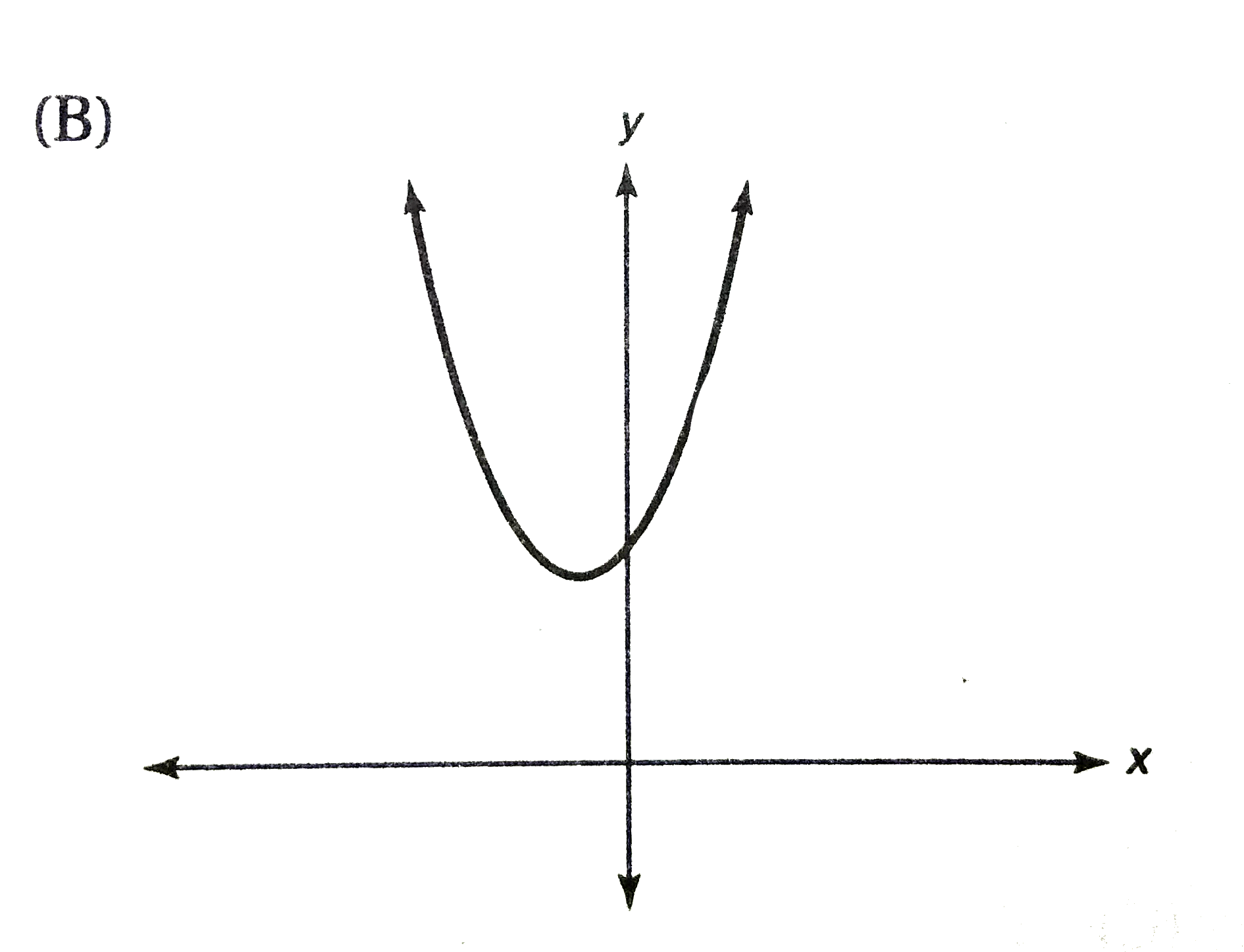 C
C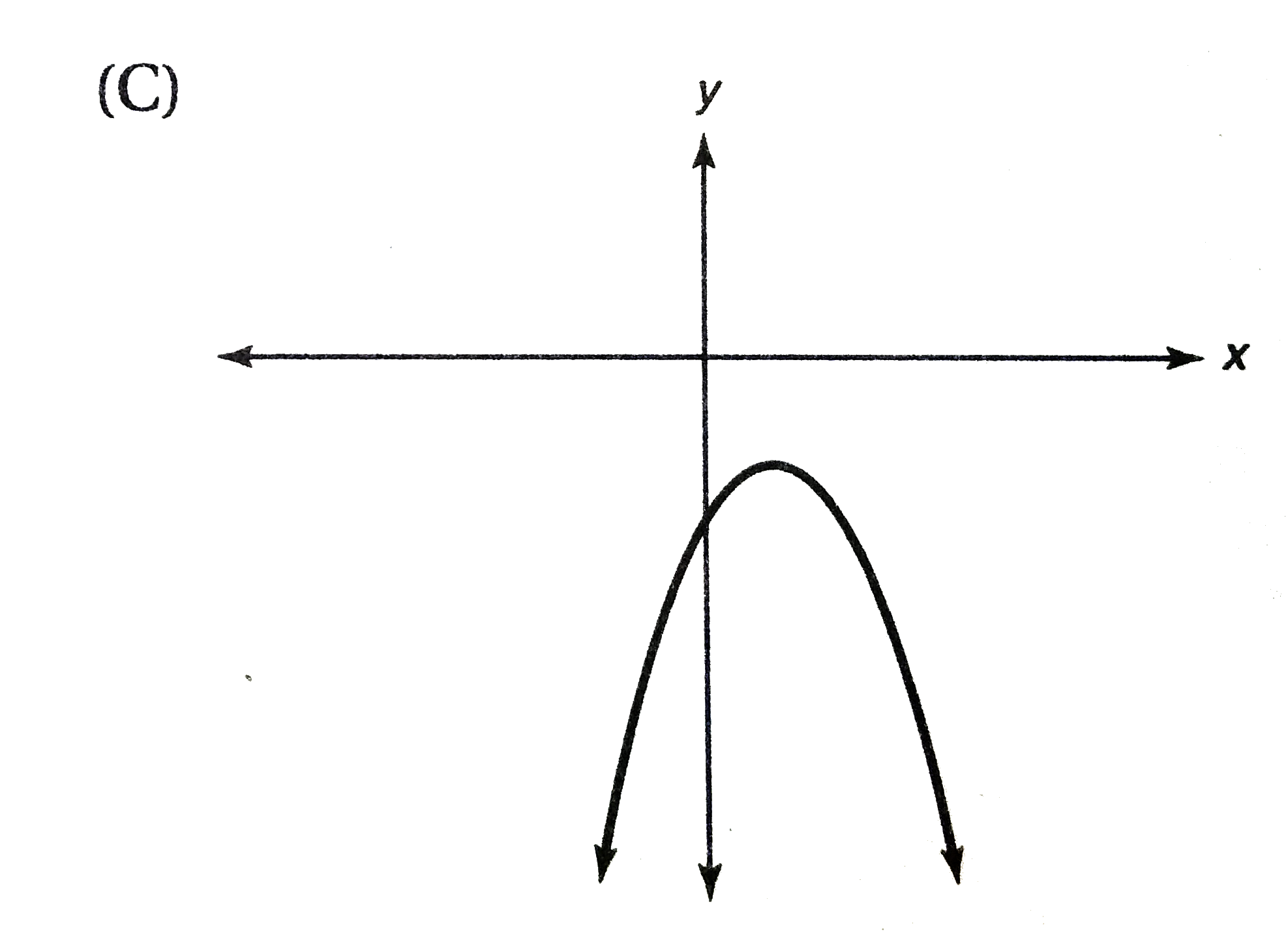 D
D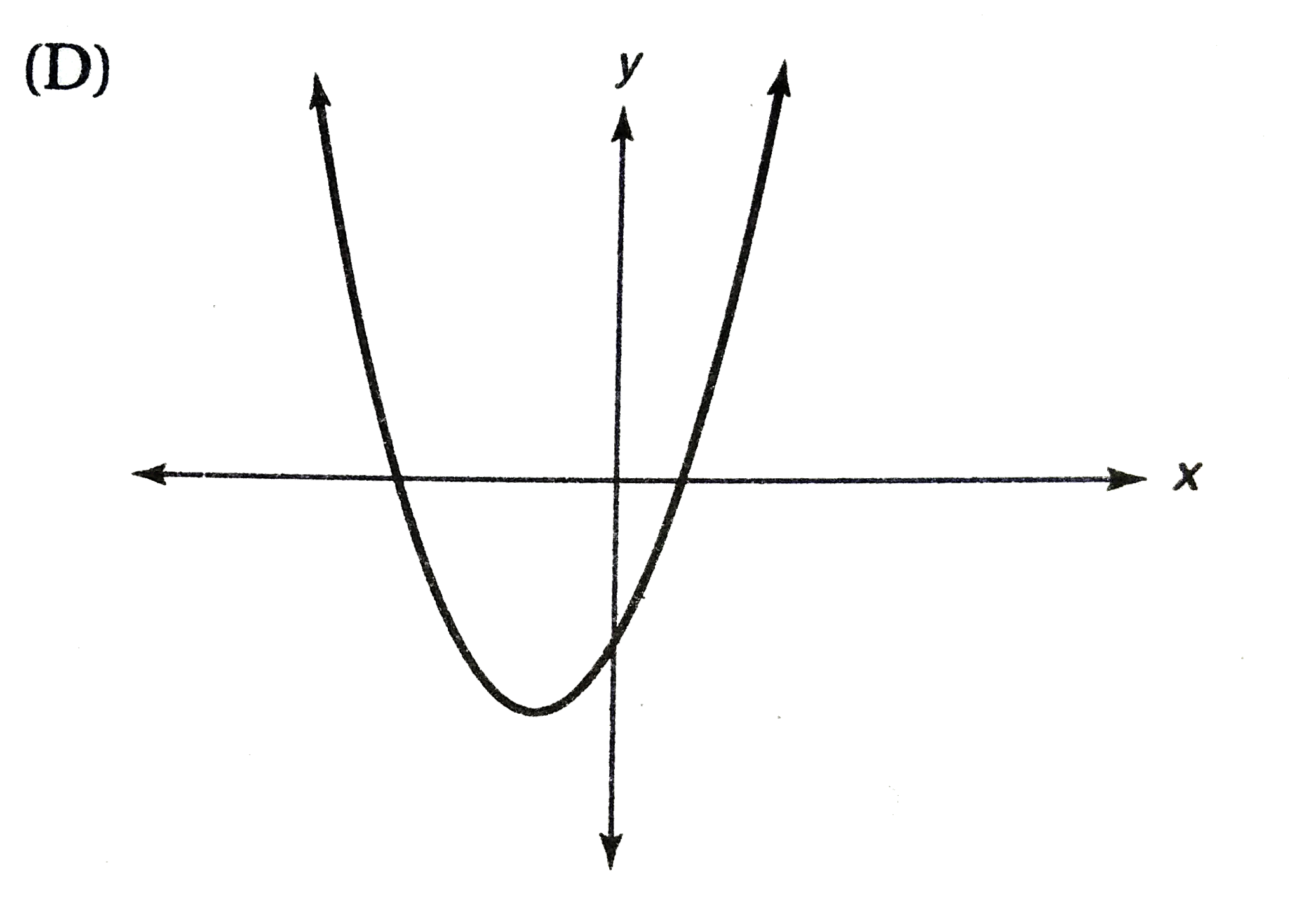
consider the function f:R→R,f(x)=x2−6x+4x2+2x+4
which of the following is not true about f(x)?
View SolutionIf f(x)=ax2+bx+c , where a≠0,b,c∈ R , then which of
the following conditions implies that f(x) has real roots?
View SolutionLet f(x)=ax2+bx+c,a>=andf(2−x)=f(2+x)∀x∈Randf(x)=0 has 2 distinct real roots, then which of the following is true ?
View SolutionIf ax2+bx+c=0andcx2+bx+a=0(a,b,c∈R) have a common non-real roots, then which of the following is not true ?
View SolutionConsider the function f:(−∞,∞)→(−∞,∞) defined by f(x)=x2−ax+1x2+ax+1;0<a<2. Which of the following is true ?
View SolutionIf x2+ax+1 is a factor of ax3+bx+c, then which of the following conditions are not valid: a. a2+c=0 b. b−a=ac c. c3+c+b2=0 d. 2c+a=b
View SolutionLet f(x) =ax3+bx2+cx+d,a≠0, where a, b, c, d∈R. If f(x) is one-one and onto, then which of the following is correct ?
View Solution

