Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.
(−∞,9)
(374,∞)
(−∞,374)
none of these
The correct Answer is:3
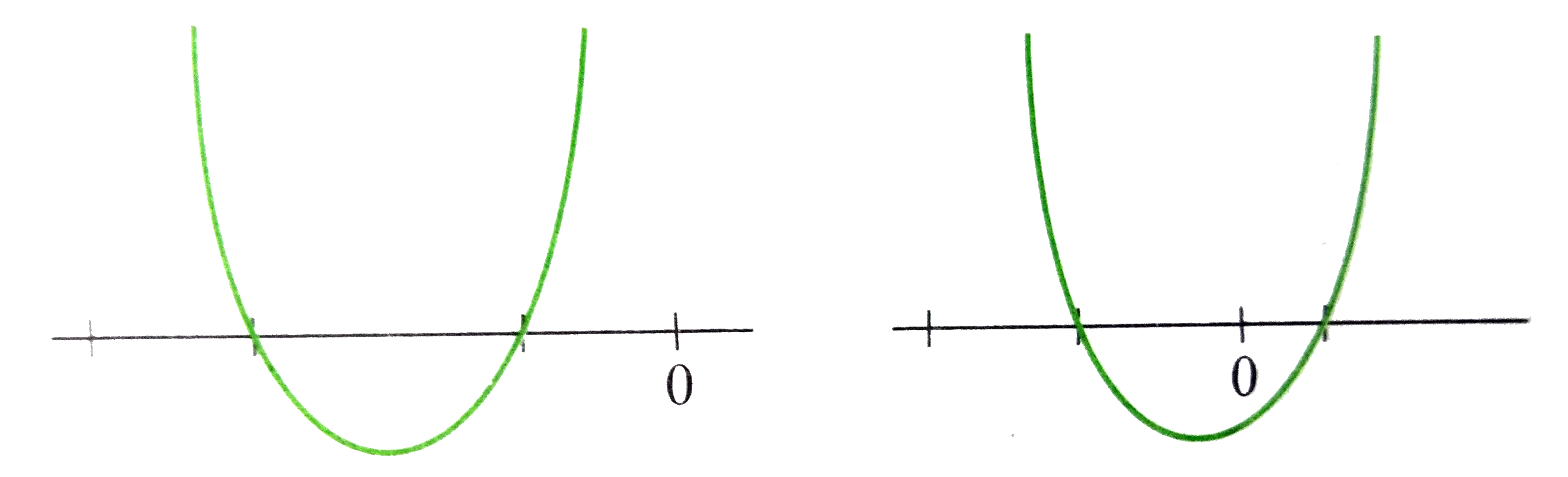
If x2+x+a−9<0 has at least one negative solution, then either both the roots of equations x2+x+a−9=0 are non-posititve or 0 lies between the roots.
For case I, sum of roots is a−9>0
⇒a>9and
D>0
⇒1−4(a−9)>0⇒a<374
Hence, 9≤a≤37/4.
For case II, f(0)>0
⇒a<9⇒a∈(−∞,374)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:
View SolutionConsider the inequation x2+x+a−9<0
The value of the parameter a so that the given inequaiton is ture ∀x∈(−1,3)
View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈ (a) (−∞,2) (b) (3,∞) (c) (−2,∞) (d) (2,3)
View SolutionSolve the inequation: 3x−2<0
View SolutionSolve the inequation 2x−3<0
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionSolve the inequation 9x5x+5<0
View SolutionSolve the inequation : 0<x3<1
View SolutionSolve the inequation (x2+x+1)x<1
View SolutionFind all the values of the parameter 'a' for which the inequality 4x−a2x−a+3≤0 is satisfied by at least one real x.
View Solution
