Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

Text Solution
The correct Answer is:a→s; b→r; c→p; d→q
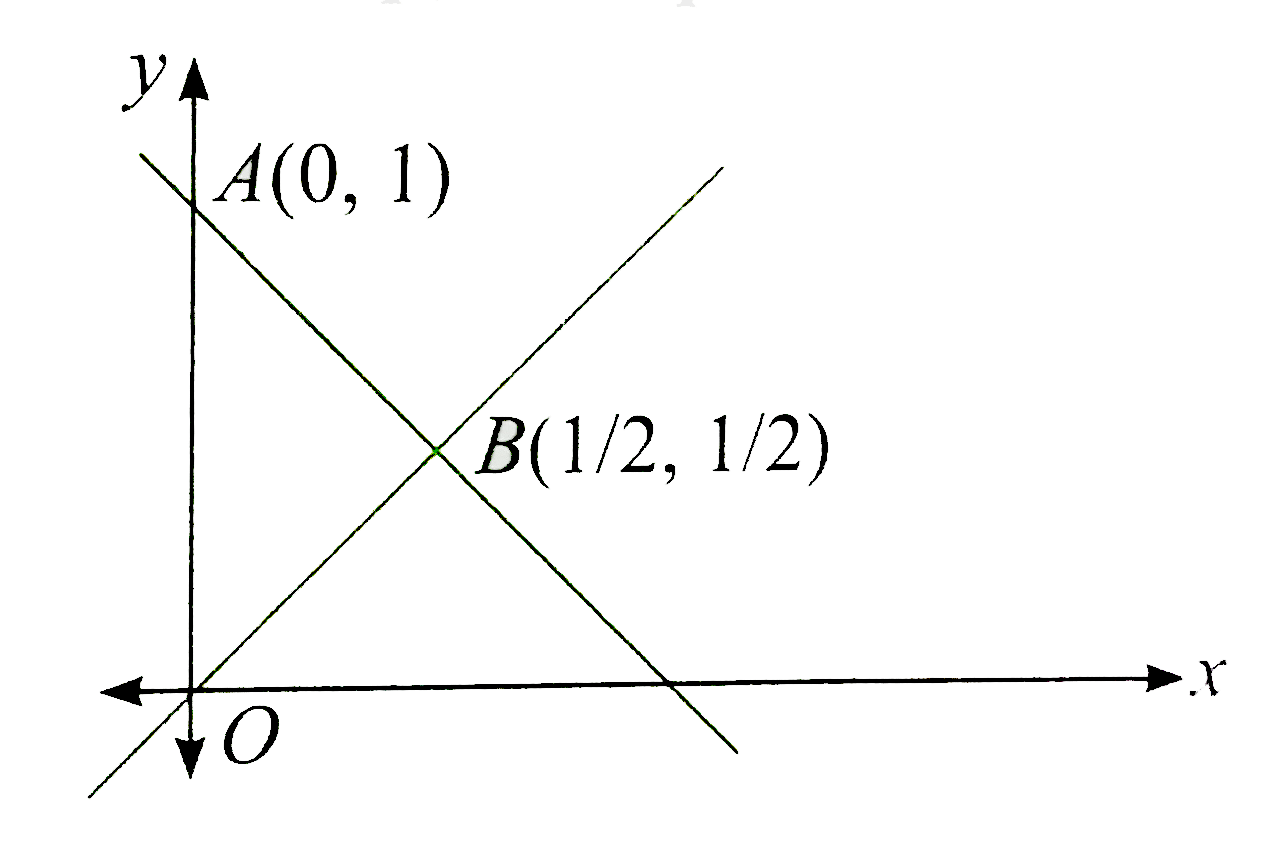
The given lines are x (x+y-1) (x-y)=0. So, lines x =0, x+y-1=0, and x-y=0 form triangle OAB as shown in the diagram.
The triangle is right-angled at pont B. Hence, the orthocenter is (1/2, 1/2). Also, the circumcenter is the midpoint of OA which is (0, 1/2). The centroid is
(0+(1/2)+03,0+(1/2)+13) or (16,12)
Also, OA=1,OB=OC=1/2√2. Hence, the incenter is
⎛⎜
⎜⎝0(1/√2)(1/2)1+0(1/√2)(1/√2)+1+(1/√2),0(1/√2)+(1/2)(1)+1(1/√2)(1/√2)+1+(1/√2)⎞⎟
⎟⎠≡(12+2√2,12)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)13videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Main Previous Year9videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two lines represented by equation x2+xy+y2=0 are
AcoincidentBparallelCmutually perpendicularDimaginary - Question 2 - Select One
The lines given by the equation (y2−4xy−x2)(x+y−1)=0 form a triangle which is
AequilateralBisoscelesCright angledDobtuse angled - Question 3 - Select One
The lines given by the equation (2y2+3xy−2x2)(x+y−1)=0 form a triangle which is
AequilateralBisoscelesCright angledDobtuse angled
The equation of the lines represented by x2+2xy−y2=0 are
View SolutionThe triangle formed by the lines whose combined equation is (y2−4xy−x2)(x+y−1)=0 is
View SolutionShow that the equation 2x2+xy−y2+x+4y−3=0 represents a pair of lines.
View SolutionThe lines represented by the equation 23x2−48xy+3y2=0 and 2x+3y+4=0 form
View SolutionIf the equation x2+3xy+2y2+x−y+k=0 represents a pair of line, then k=
View Solution

