Consider the lines represented by equation $(x^{2} + x y - x) \times (x - y) = 0$ forming a triangle. Then match the following lists:
Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a top;btop,s;ctop,r;dtoq,s

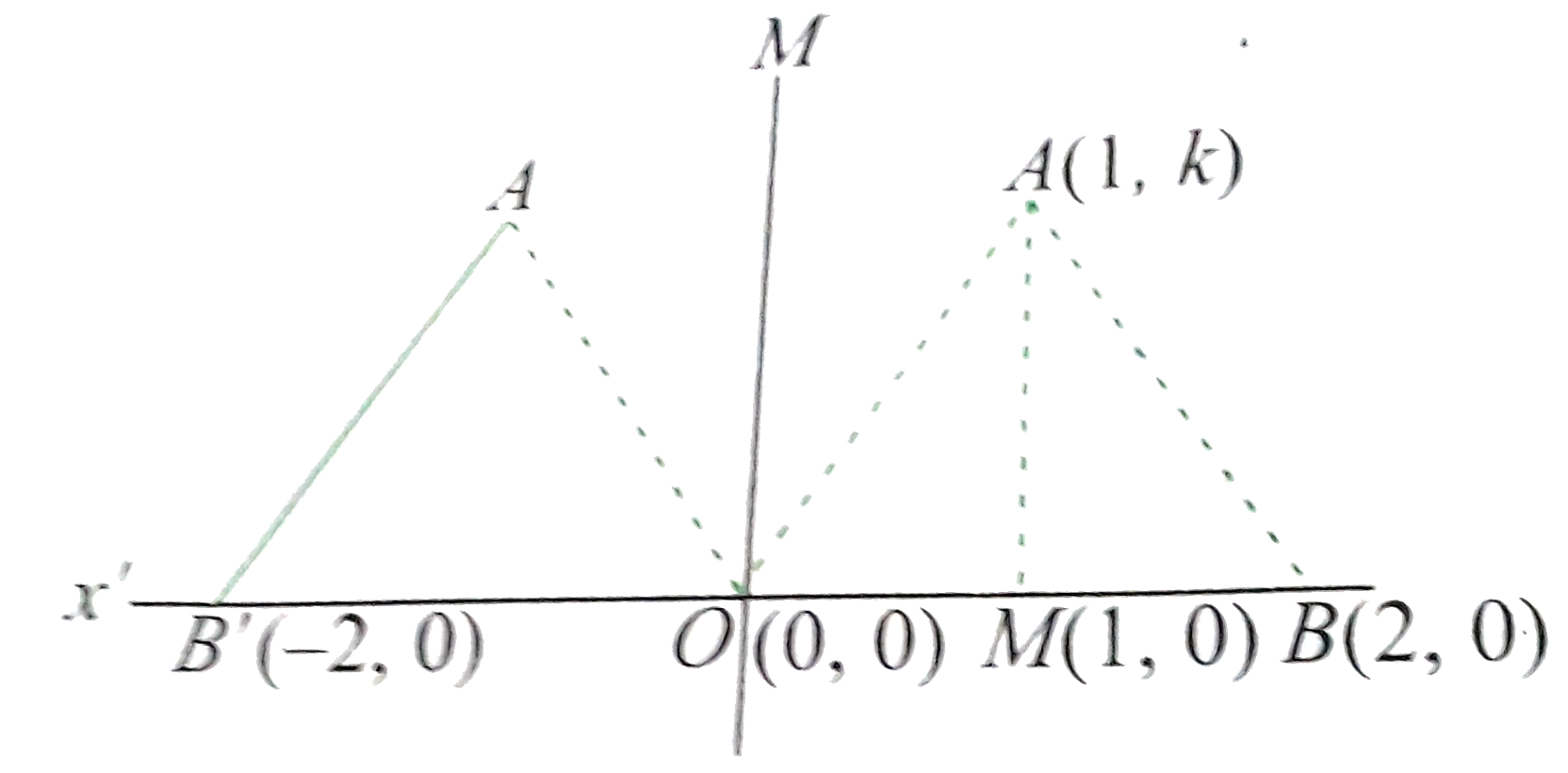
From the figure , $Δ A B C$ is equilateral. Hence,
${tan 60}^{\circ} = k$
i.e., $k = \sqrt{3}$ (for first quadrant)
or $k = - \sqrt{3}$ (for fourth quadrant)
then the possible coordinates are $(1, \pm \sqrt{3})$ .
Similarly , for the second quadrant, the point is $(- 1, \sqrt{3})$ and for the third quadrant , the point is $(- 1, - \sqrt{3})$ .
(b) Case i :
If $O A = A B$ , then $∠ A = 30^{\circ}$ , Therefore

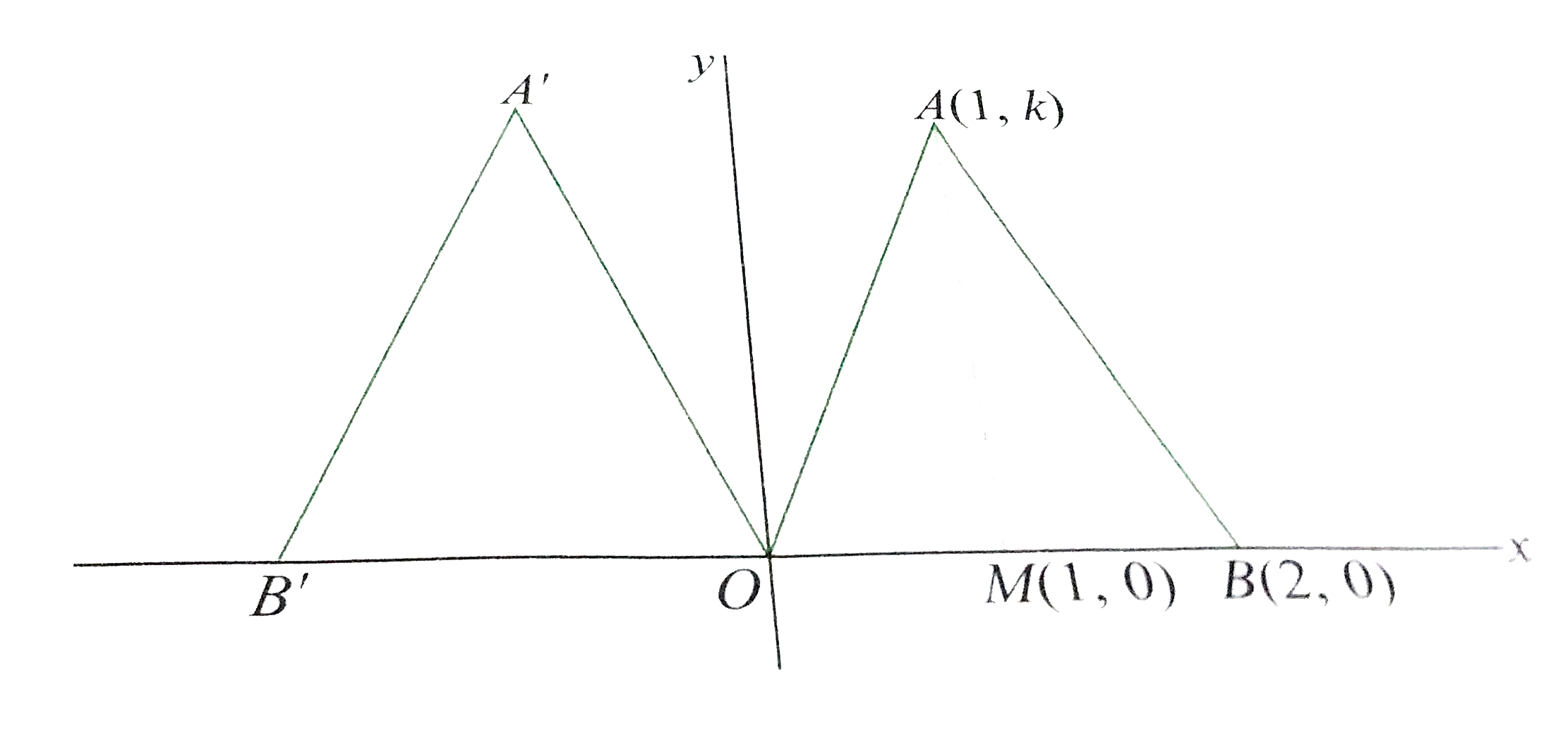
$∠ A O B = 75^{\circ}$
$∴ \frac{A M}{O M} = {tan 75}^{\circ}$
$A M = O M {tan 75}^{\circ}$
$k = 1 \times (2 + \sqrt{3})$
$∴ k = 2 + \sqrt{3}$
Hence, point A is $(1, 2 + \sqrt{3})$ . By symmetry, all possible points are $(\pm 1, \pm (2 + \sqrt{3}))$ .
Case ii:
$A O = O B$
$∴ ∠ A O B = 120^{\circ}$

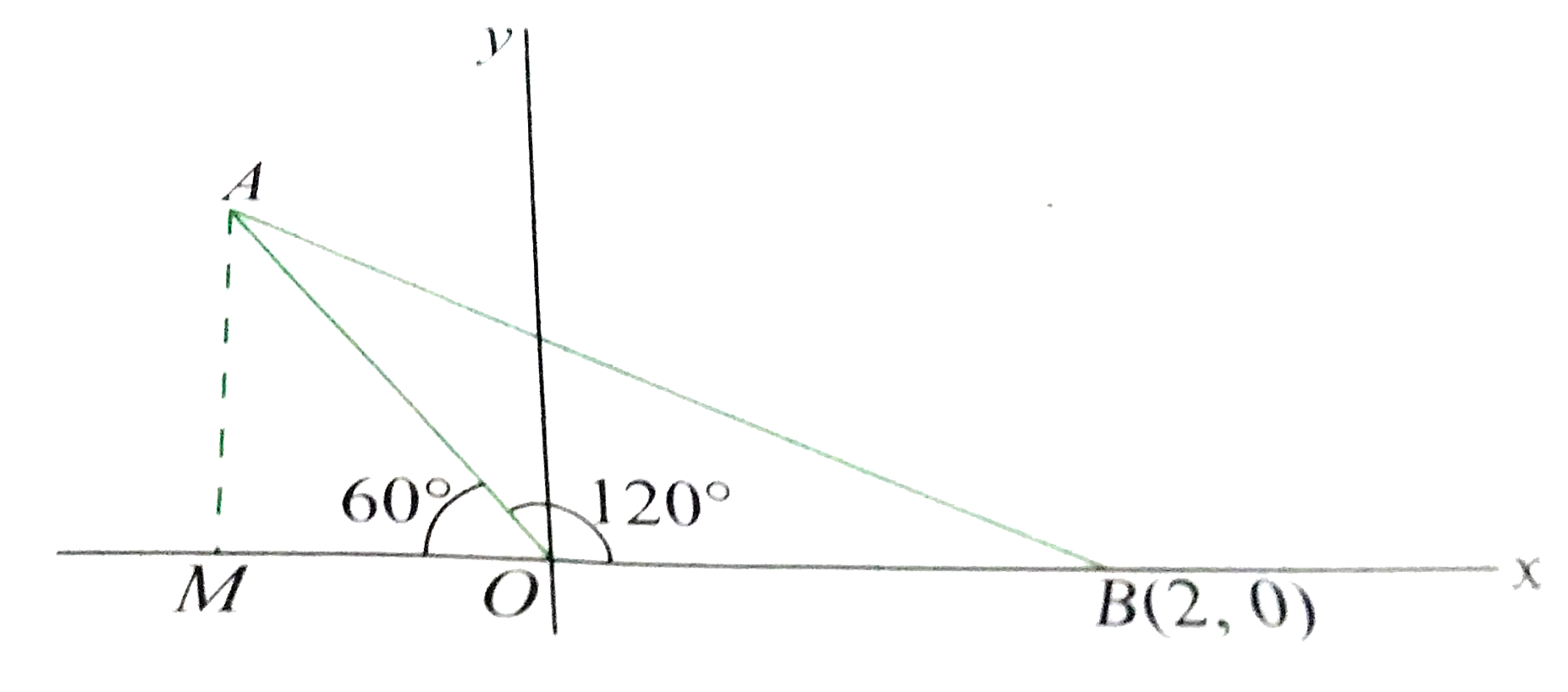
$A M = 2 {sin 60}^{\circ} = \sqrt{3}$
and $O M = 2 {cos 60}^{\circ} = 1$
Hence, point A is $(- 1, - \sqrt{3})$ , By symmetry, all possible points are $(\pm 1, \pm \sqrt{3})$ .
(c).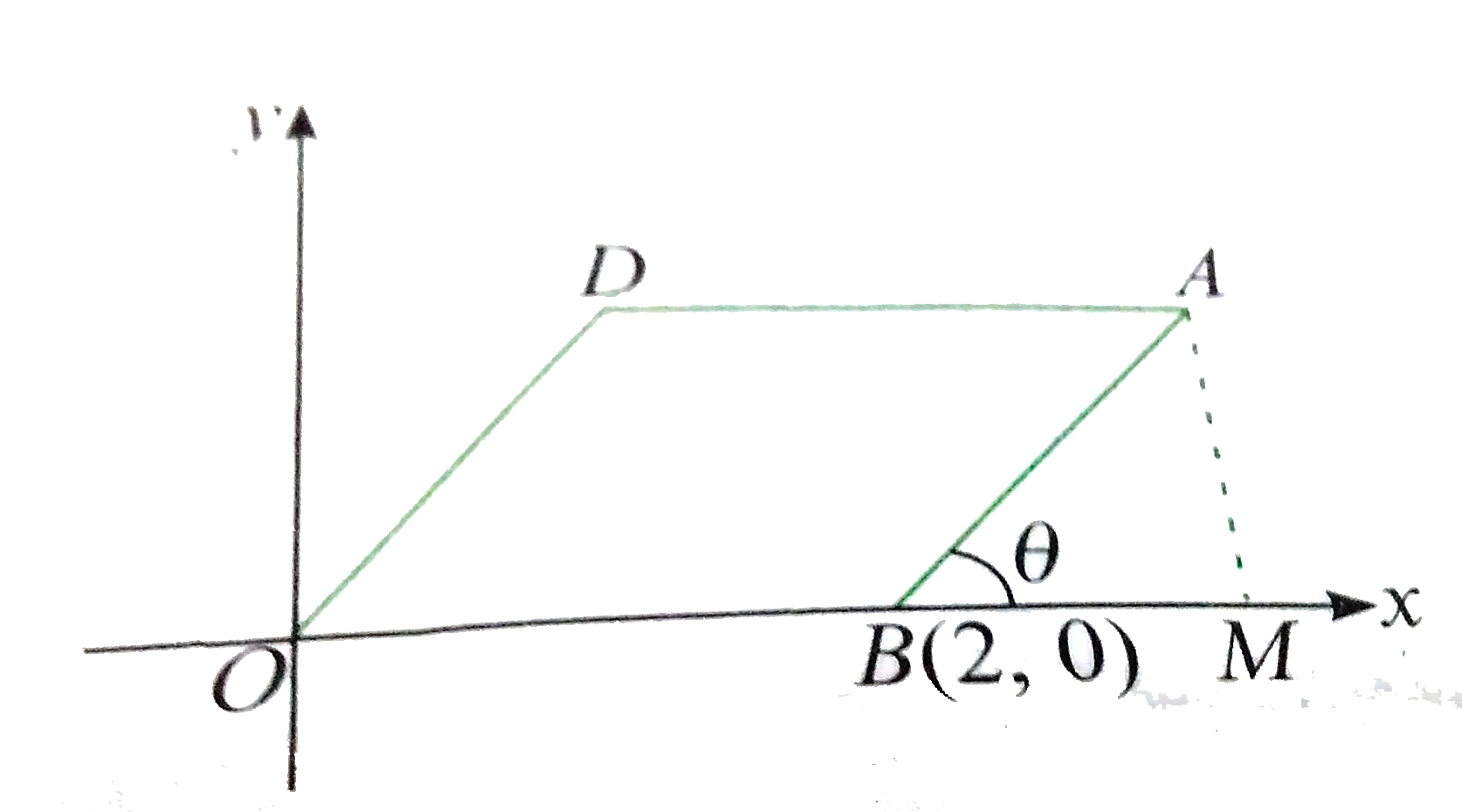
Let $∠ D O B = ∠ A B M = θ$ .
Area of $Δ O A B = \frac{1}{2} \times O B \times A M = \frac{1}{2} \times 2 \sqrt{3}$
or $2 \times 2 sin θ = 2 \sqrt{3}$
or $sin θ = \frac{\sqrt{3}}{2}$
or $A M = \sqrt{3} and B M = 1$
Hence, A has coordinates $(3, \sqrt{3})$ , By symmetry, all the possible coordinates are $(\pm 3, \pm \sqrt{3})$ .

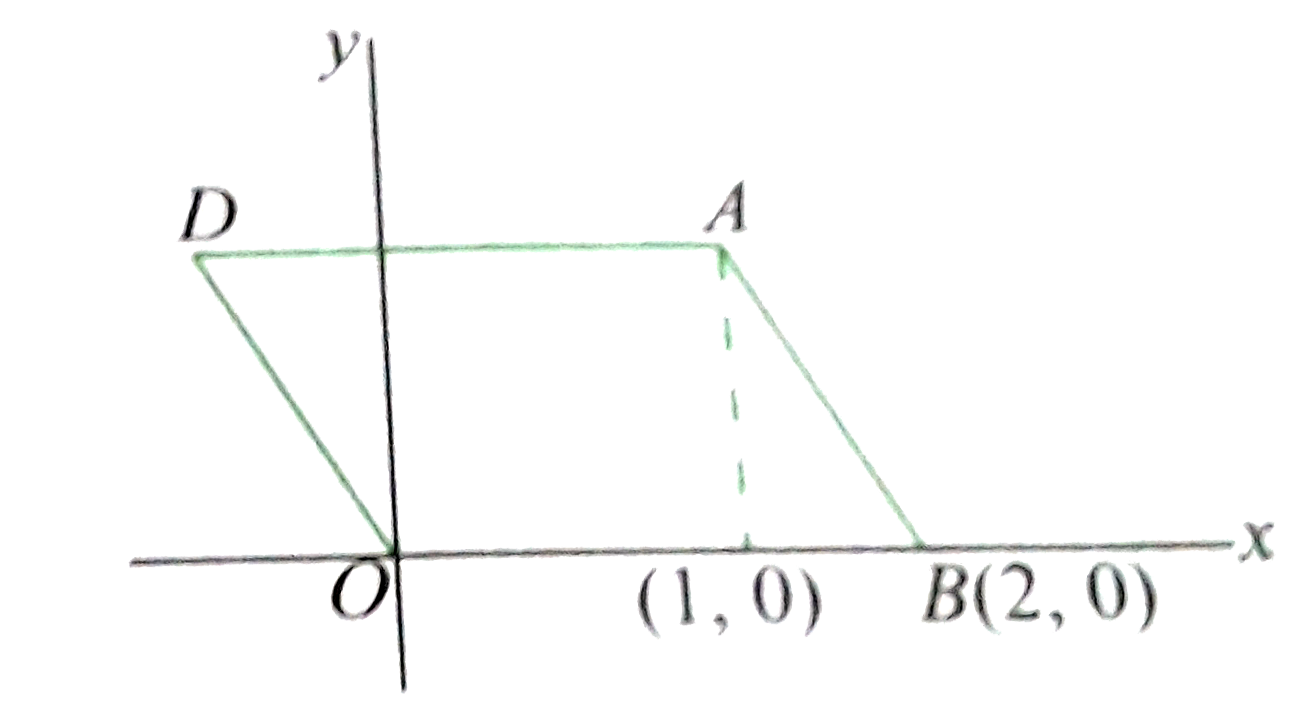
From the figure, A has coordinates $(1, \sqrt{3})$ .
By symmetry, all possible coordinates are $(\pm, \pm \sqrt{3})$ .
(d)
$O B = 2 u n i t s = O O' = Radius$
or $O M = \frac{2}{2} = 1 unit$
In $Δ O O' M$ ,
$O' M = \sqrt{4 - 1} = \sqrt{3}$
Since $Δ O A B$ is isosceles, point A lies on the perpendicular bisector of OB. Therefore,
$A M = \sqrt{3} + 2 = O M + O A$
Hence, the coordinates of A will be $(1, 2 + \sqrt{3})$ in the first quadrant. By symmetry, all possible coordinates of A are $(\pm 1, \pm (2 + \sqrt{3})$ .

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-COORDINATE SYSYEM -Matrix match type

Home
Ask Doubt
Profile