For points P=(x1,y1)and Q=(x2,y2) of the co-ordinate plane a new distance d(P,Q)=|x1−x2|+|y1−y2| is defined .Let O(0,0)and A(3,2). The set of points in first quadrant which are equidistant from O and A is Solution in Bengali
one straight line only
union of two line segments
union of two infinite rays
union of a line segment of finite length and an infinite ray
The correct Answer is:D
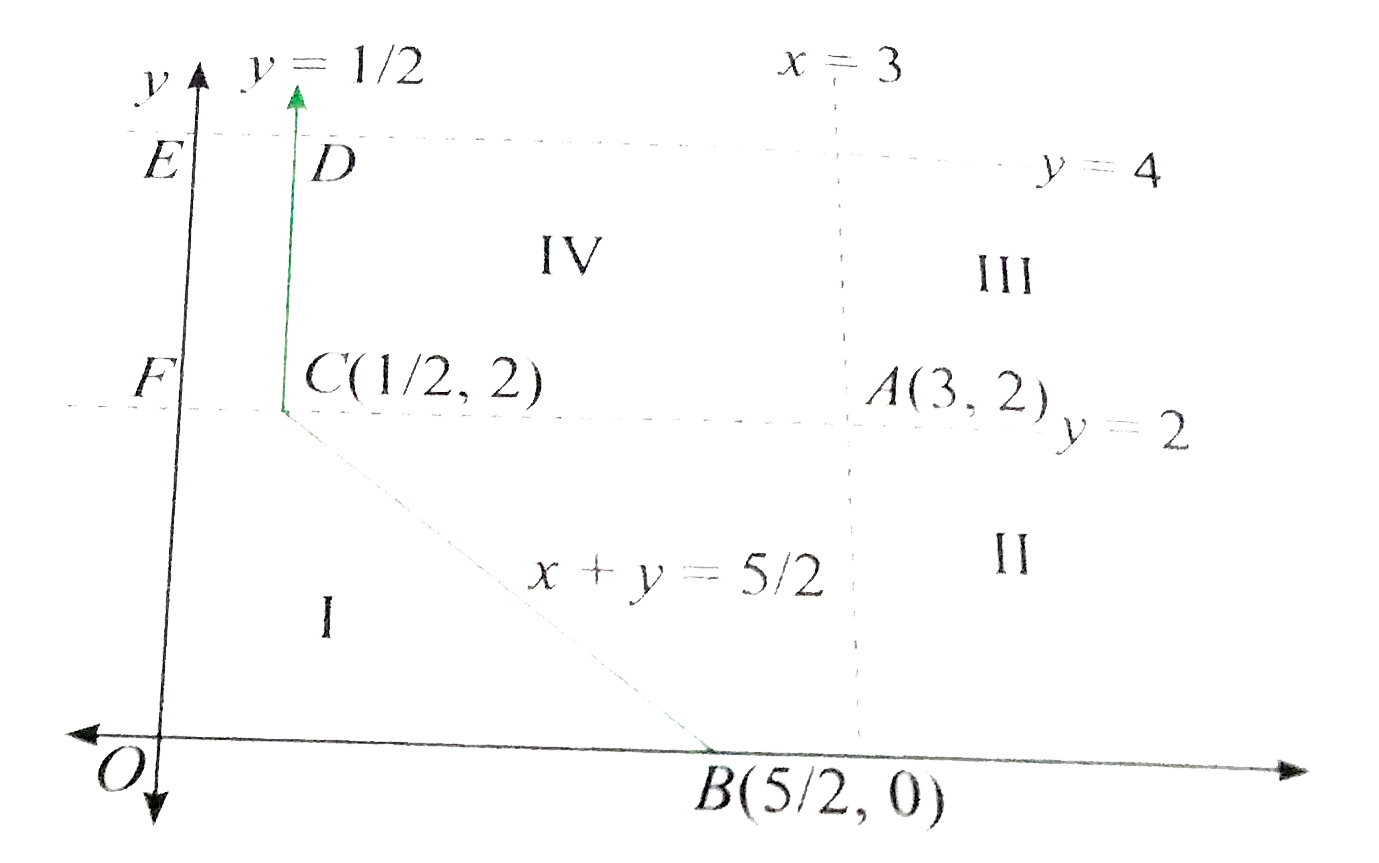
Obviously, the locus of P is the union of line segment and one infinite ray.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type4videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value12videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:
 10:03View Solution
10:03View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
01:37View SolutionIf (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
03:06View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
01:47View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
02:54View SolutionFor points P = (x_1, y_1) and Q = (x_2,y_2) of the coordinate plane, a new distance d (P, Q) is defined by d(P,Q)=|x_1-x_2|+|y_1-y_2|. Let O (0, 0) and A = (3, 2) . Prove that the set of points in the first quadrant which are equidistant (wrt new distance) from O and A consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.
View SolutionThe ratio in which the line segment joining P(x1, y1) and Q(x2, y2) is divided by x-axis is y1:y2 (b) y1:y2 (c) x1:x2 (d) x1:x2
05:20View SolutionIf the point x1+t(x2−x1),y1+t(y2−y1) divides the join of (x1,y1) and (x2,y2) internally then
06:22View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The set of poitns P consists of02:12View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The area of the ragion bounded by the locus of P and the line y=4 in the first quadrant is03:26View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d(P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The locus of point P is02:33View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinate plane, a new distance d(P,Q)=|x1−x1|+|y1−y2|. Let O=(0,0) and A=(3,2) . Prove that the set of points in the first quadrant which are equidistant (with respect to the new distance) from O and A consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.
05:42View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The set of poitns P consists of05:02View SolutionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The area of the ragion bounded by the locus of P and the line y=4 in the first quadrant is07:47View SolutionThe ratio in which the line segment joining P(x1, y1) and Q(x2, y2) is divided by x-axis is (a) y1:y2 (b) y1:y2 (c) x1:x2 (d) x1:x2
03:17View SolutionIf the points P(h,k), Q(x1,y1)and R(x2,y2) lie on a line. Show that: (h−x1)(y2−y1)=(k−y1)(x2−x1).
05:24View Solution

