Consider the regions A={(x,y)∣x2+y2≤100} and ={(x,y)∣sin(x+y)>0} in the plane. Then the area of the region A∩B is -
A
10π
B
100
C
100π
D
50π
Text Solution
The correct Answer is:D
x2+y2≤100→inside of a circle
sin(x+y)>0
x+y∈(x,π)∪(2π,3π)…….
x+y=c→equation of a line
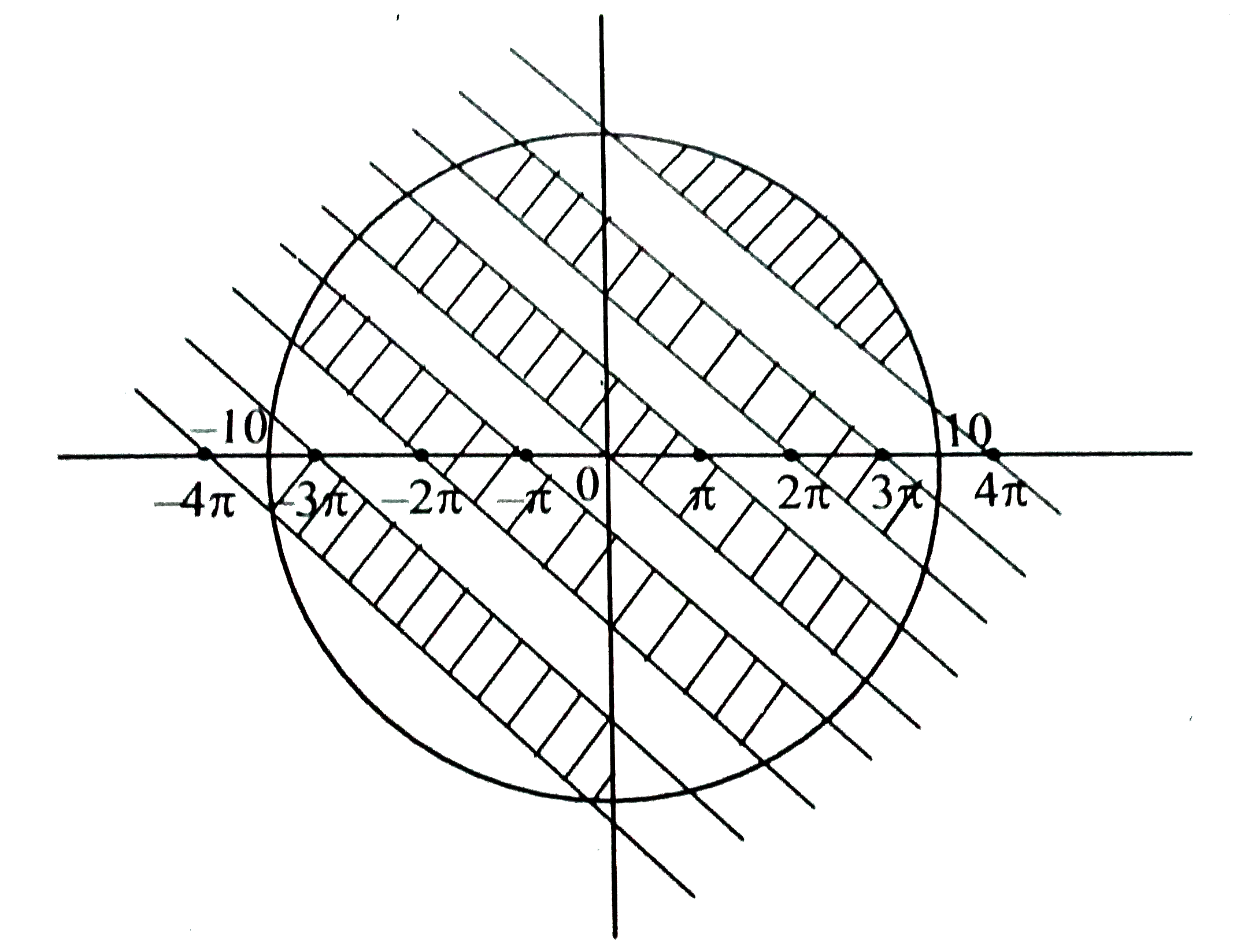
required area = shaded region =12π(10)2=50π
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the regions A={(x,y)∣x2+y2≤100}andB=|xy|sin(x+y)>0} in the plane. Then the area of the region A∩B is
A10πB100C100πD50πThe area of the region {(x,y):x2+y2≤1≤x+y} , is
Aπ5Bπ4Cπ24Dπ4−12The area of the region described by A={(x,y):x2+y2≤1 and y2≤1−x} is :
Aπ2−23Bπ2+23Cπ2+43Dπ2+43
Find the area of the region {(x,y):x2+y2≤1≤x+y}
View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
View SolutionThe area of the region {(x,y):x2+y2≤5,||x|−|y∣∣≥1 is
View SolutionLet A={(x,y):y2≤4x,y−2x≥−2,y≥0}. The area of the region A is
View SolutionThe area of the region R={(x,y):|x|≤|y|andx2+y2≤1} is
View Solution
