Consider triangle ABC as shown in the figure
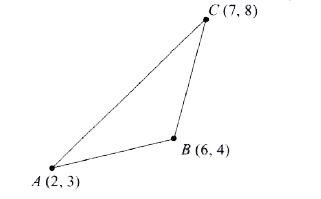
The new vertices of triangle when it undergoes the transformation (XY)=⎛⎝−1311−13⎞⎠(xy) will be
A'≡(73,1),B'≡(2,143),C'≡(173,133)
A'≡(73,1),B'≡(143,2),C'≡(173,133)
A'≡(73,1),B'≡(2,143),C'≡(133,133)
A'≡(1,73),B'≡(2,143),C'≡(173,133)
The correct Answer is:A
Topper's Solved these Questions
- TRANSFORMATIONSBOOK - CENGAGECHAPTER - TRANSFORMATIONSEXERCISE - Olympiad and NTSE level exercises
10 Videos
- TRANSFORMATIONSBOOK - CENGAGECHAPTER - TRANSFORMATIONSEXERCISE - Test yourself (Level 1)
18 Videos
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- TRIGONOMETRY BOOK - CENGAGECHAPTER - TRIGONOMETRY EXERCISE - WORKED EXAMPLES
4 Videos
Similar Questions
Knowledge Check
If all the vertices of a triangle undergo the same transfomation (XY)=(12−1211)(xy) what will be the effect on the area of the triangle ?
AIt will remain unchangedBIt will become halfCIt will become 0DIt will get doubleConsider the ΔABC with vertices A( - 2 , 3) , B (2 , 1) and C (1 ,2)
What is the Centroid of the ΔABC ?A(13,2)B(2,2)C(−2,2)D(2,−2)Consider the ΔABC with vertices A( - 2 , 3) , B (3 , 1) and C (1 ,2)
What is the centroid of the ΔABC ?A(23,2)B(13,2)C(1,23)D(12,3)
The centroid of the triangle with vertices at A(x1,y1),B(x2,y2),c(x3,y3) is
View SolutionIn a triangle ABC,A(1,3) and perpendicular bisector of AB is y=x and orthocentre of triangle ABC is (3,1), then locus of vertex C is
View SolutionIf the coordinates of the vertices of an equilateral triangle with sides of length a are (x1,y1),(x2,y2) and (x3,y3) then ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=3a44
View SolutionIf the coordinates of the vertices of an equilateral triangle with sides of length a are (x1,y1),(x2,y2) and (x3,y3) then ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=3a44
View SolutionIf A(x1,y1),B(x2,y2) and C(x3,y3) are the vertices of a ΔABC and (x, y) be a point on the internal bisector of angle A, then prove that
b∣∣ ∣ ∣∣xy1x1y11x2y21∣∣ ∣ ∣∣+c∣∣ ∣ ∣∣xy1x1y11x3y31∣∣ ∣ ∣∣=0
where, AC = b and AB = c.
View Solution
