Consider △ABC and △A1B1C1 in such a way that ¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯A1B1 and M,N,M1,N1 be the midpoints of AB,BC,A1B1andB1C1 respectively, then
−−−→MM1=−−−→NN1
−−→CC1=−−−→MM1
−−→CC1=−−−→NN1
−−−→MM1=−−→BB1
The correct Answer is:D
To solve the problem involving triangles ABC and A1B1C1 with the given conditions, we can follow these steps:
Step 1: Define the Points
Let the coordinates of the points be:
- A(x1,y1)
- B(x2,y2)
- C(x3,y3)
- A1(x′1,y′1)
- B1(x′2,y′2)
- C1(x′3,y′3)
Given that ¯¯¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯¯¯¯¯A1B1, we have:
√(x2−x1)2+(y2−y1)2=√(x′2−x′1)2+(y′1−y1)2
Step 2: Find the Midpoints
The midpoints M and N of segments AB and BC respectively are given by:
M=(x1+x22,y1+y22)
N=(x2+x32,y2+y32)
Similarly, the midpoints M1 and N1 of segments A1B1 and B1C1 are:
M1=(x′1+x′22,y′1+y′22)
N1=(x′2+x′32,y′2+y′32)
Step 3: Establish Relationships
Since ¯¯¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯¯¯¯¯A1B1, we can establish relationships between the midpoints:
¯¯¯¯¯¯¯¯¯¯¯MN=¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1
Step 4: Calculate Vectors
The vector from M to N is:
¯¯¯¯¯¯¯¯¯¯¯MN=N−M=(x2+x32−x1+x22,y2+y32−y1+y22)
This simplifies to:
¯¯¯¯¯¯¯¯¯¯¯MN=(x3−x12,y3−y12)
Similarly, for M1 and N1:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1=N1−M1=(x′2+x′32−x′1+x′22,y′2+y′32−y′1+y′22)
This simplifies to:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1=(x′3−x′12,y′3−y′12)
Step 5: Show Equality of Vectors
Since ¯¯¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯¯¯¯¯A1B1, the lengths and directions of the vectors must be equal. Therefore:
¯¯¯¯¯¯¯¯¯¯¯MN=¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1
This implies:
\frac{x_3 - x_1}{2} = \frac{x_3' - x_1'}{2} \quad \text{and} \quad \frac{y_3 - y_1}{2} = \frac{y_3' - y_1'}
Conclusion
Thus, we conclude that the midpoints M and M1 are related as follows:
M=M1andN=N1
This leads us to the conclusion that option D is correct:
M=M1andN=N1
Let the coordinates of the points be:
- A(x1,y1)
- B(x2,y2)
- C(x3,y3)
- A1(x′1,y′1)
- B1(x′2,y′2)
- C1(x′3,y′3)
√(x2−x1)2+(y2−y1)2=√(x′2−x′1)2+(y′1−y1)2
The midpoints M and N of segments AB and BC respectively are given by:
M=(x1+x22,y1+y22)
N=(x2+x32,y2+y32)
M1=(x′1+x′22,y′1+y′22)
N1=(x′2+x′32,y′2+y′32)
Since ¯¯¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯¯¯¯¯A1B1, we can establish relationships between the midpoints:
¯¯¯¯¯¯¯¯¯¯¯MN=¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1
The vector from M to N is:
¯¯¯¯¯¯¯¯¯¯¯MN=N−M=(x2+x32−x1+x22,y2+y32−y1+y22)
This simplifies to:
¯¯¯¯¯¯¯¯¯¯¯MN=(x3−x12,y3−y12)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1=N1−M1=(x′2+x′32−x′1+x′22,y′2+y′32−y′1+y′22)
This simplifies to:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1=(x′3−x′12,y′3−y′12)
Since ¯¯¯¯¯¯¯¯AB=¯¯¯¯¯¯¯¯¯¯¯¯¯A1B1, the lengths and directions of the vectors must be equal. Therefore:
¯¯¯¯¯¯¯¯¯¯¯MN=¯¯¯¯¯¯¯¯¯¯¯¯¯¯M1N1
This implies:
\frac{x_3 - x_1}{2} = \frac{x_3' - x_1'}{2} \quad \text{and} \quad \frac{y_3 - y_1}{2} = \frac{y_3' - y_1'}
Thus, we conclude that the midpoints M and M1 are related as follows:
M=M1andN=N1
This leads us to the conclusion that option D is correct:
M=M1andN=N1
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Exercise30videos
ALGEBRA OF VECTORS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test30videos
ALGEBRA OF VECTORS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise39videos
ALGEBRAIC INEQUATIONS
Similar Questions
Given a cube ABCD A1B1C1D1 which lower base ABCD, upper base A1B1C1D1 and the lateral edges AA1,BB1,CC1 and DD1 M and M1 are the centres of the forces ABCD and A1B1C1D1 respectively. O is a point on the line MM2 such that ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB,¯¯¯¯¯¯OC+¯¯¯¯¯¯OD=¯¯¯¯¯¯¯OM, then ¯¯¯¯¯¯¯OM=λ(OM1) is equal to
View Solution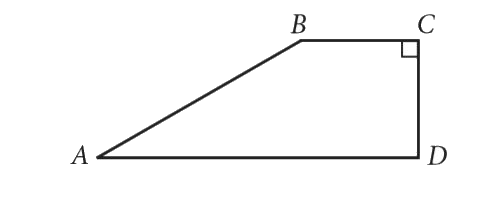
In quadrilateral ABCD above , ¯¯¯¯¯¯AD¯¯¯¯¯¯BC and CD=12AB. What is the measure of angle B ?View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. limn→∞∠An=View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:View SolutionIf the midpoint of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC are (3, -3), (3, -1), (1, 1) respectively then the vertices A, B, C are
View SolutionAB is a double ordinate of the parabola y2=4ax. Tangents drawn to the parabola at AandB meet the y-axis at A1andB1 , respectively. If the area of trapezium ∀1B1B is equal to 12a2, then the angle subtended by A1B1 at the focus of the parabola is equal to 2tan−1(3) (b) tan−1(3) 2tan−1(2) (d) tan−1(2)
View SolutionLet X=A.¯¯¯¯¯¯BC . Evaluate X for
(a) A=1,B=0,C=1, (b) A = B = C = 1 and ( c) A = B = C = 0.View SolutionABC is a right-angled triangle in which ∠B=900 and BC=a. If n points L1,L2,,LnonAB is divided in n+1 equal parts and L1M1,L2M2,,LnMn are line segments parallel to BCandM1,M2,,Mn are on AC, then the sum of the lengths of L1M1,L2M2,,LnMn is a(n+1)2 b. a(n−1)2 c. an2 d. none of these
View SolutionIf A1B1 and A2B2 are two focal chords of the parabola y2=4ax, then the chords A1A2 and B1B2 intersect on directrix (b) axis tangent at vertex (d) none of these
View Solution1a,1band1c are in A.P. Show that bc, ca, and ab are also in A.P.
View Solution

