Construct a quadrilateral ABCD given AB=5.6cm, BC=4.1cm, CD=4.4cm, AD=3.3cm and ∠A=750.
Steps of Construction:
(1)DrawAB =5.6cm
(2)Construct ∠BAX=75°.
(3) With A as centre and radius AD= 3.3cm, cut offAD=3.3cm
(4) Join BD
(5)With Das centre and radius DC=4.4cm, draw an arc
(6) With B as centre and radiusBC=4.1cm, drawn an arc to cut drawn in step (5) at C.
JoinBC CD to obtain the required quadrilateral ABCD.
Topper's Solved these Questions
Similar Questions
Which of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View Solution
Knowledge Check
In a cyclic quadrilateral ABCD∠A+∠B+∠C+∠D=?
AA)90∘BB)360∘CC)180∘DD)120∘
Calculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=
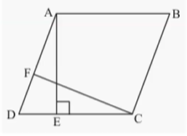
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionIn fig. 15 ABCD is a parallelogram CM⊥AB and BL⊥AD. If AB=16 cm, AD=12 cm, CM=10 cm, find BL If AD=10cm, CM=8cm, BL=12 cm, find AB .
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View Solution
