Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F-4x+6y be the objective function. Determine the minimum valur of F occurs at
only (0,2)
only (3,0)
the mid point of the line segment joining the points (0,2) and (3,0)
any point of the line segemet joining the points (0,2) and (3,0)
The correct Answer is:D
To determine the minimum value of the objective function F=4x+6y at the corner points of the feasible region, we will evaluate F at each of the given corner points: (0,2), (3,0), (6,0), (6,8), and (0,5).
1. Evaluate F at (0, 2):
F(0,2)=4(0)+6(2)=0+12=12
2. Evaluate F at (3, 0):
F(3,0)=4(3)+6(0)=12+0=12
3. Evaluate F at (6, 0):
F(6,0)=4(6)+6(0)=24+0=24
4. Evaluate F at (6, 8):
F(6,8)=4(6)+6(8)=24+48=72
5. Evaluate F at (0, 5):
F(0,5)=4(0)+6(5)=0+30=30
Summary of Values:
- At (0,2), F=12
- At (3,0), F=12
- At (6,0), F=24
- At (6,8), F=72
- At (0,5), F=30
Conclusion:
The minimum value of F occurs at the points (0,2) and (3,0), both giving F=12.
F(0,2)=4(0)+6(2)=0+12=12
F(3,0)=4(3)+6(0)=12+0=12
F(6,0)=4(6)+6(0)=24+0=24
F(6,8)=4(6)+6(8)=24+48=72
F(0,5)=4(0)+6(5)=0+30=30
- At (0,2), F=12
- At (3,0), F=12
- At (6,0), F=24
- At (6,8), F=72
- At (0,5), F=30
The minimum value of F occurs at the points (0,2) and (3,0), both giving F=12.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - TRUE/FALSE
2 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - TRUE/FALSE
2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
Corner points of the feasible region for an LPP are ( 0,2) (3,0) ,(6,0),(6,8) and (0,5) Let Z=4 x + 6y be the objective function. The minimum value of F occurs at?
View SolutionThe corner points of the feasible region of an LPP are (0,0), (0,8), (2,7),(5,4),and (6,4). the maximum profit P= 3x + 2y occurs at the point_____.
View Solution
Knowledge Check
If the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
AA) (0, 2) onlyBB) (3, 0) onlyCC) the mid-point of the line segment joining the point (0, 2) and (3, 0) onlyDD) every point on the line segment joining the point (0, 2) and (3, 0)If the corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8),(0,5) then maximum of F - minimum of F =
A60B48C42D18The occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
Ap=2qBp=q2Cp=3qDp=q
The feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is
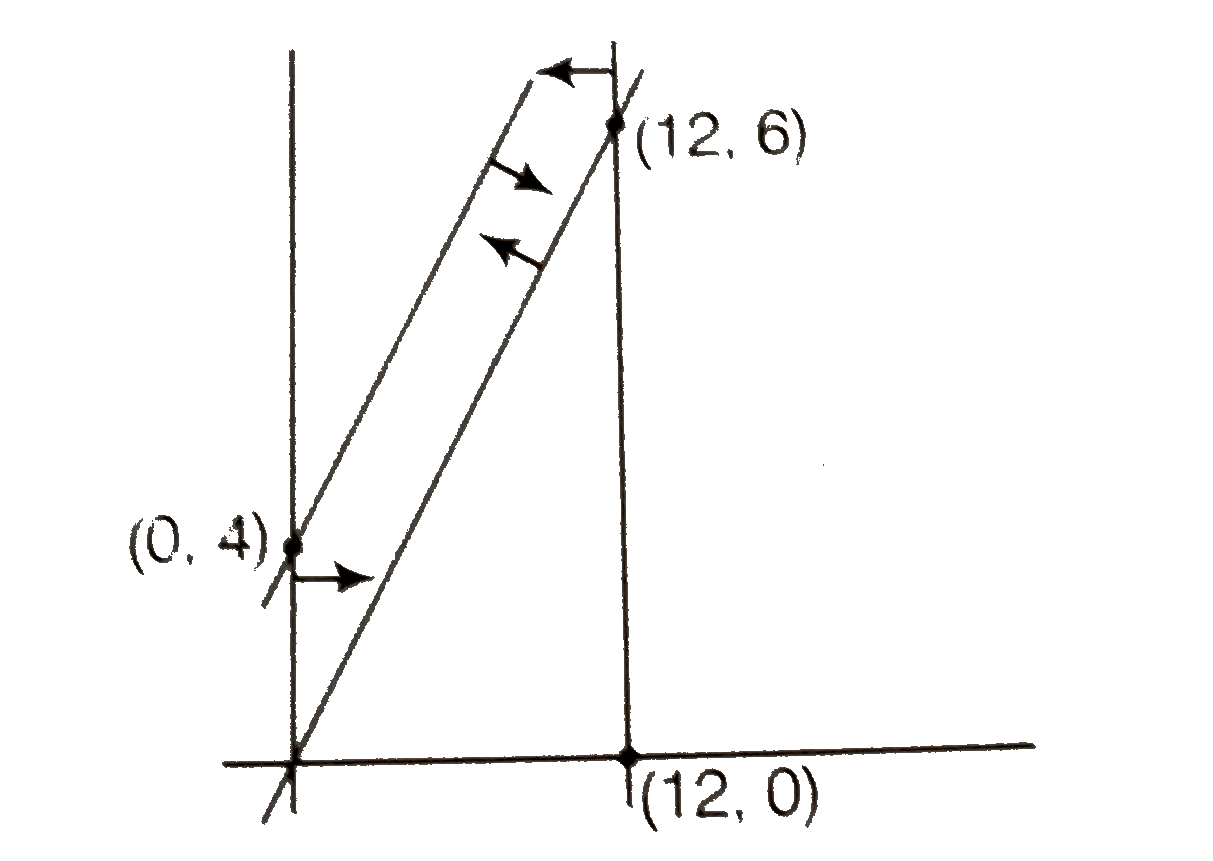
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
View SolutionThe feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at
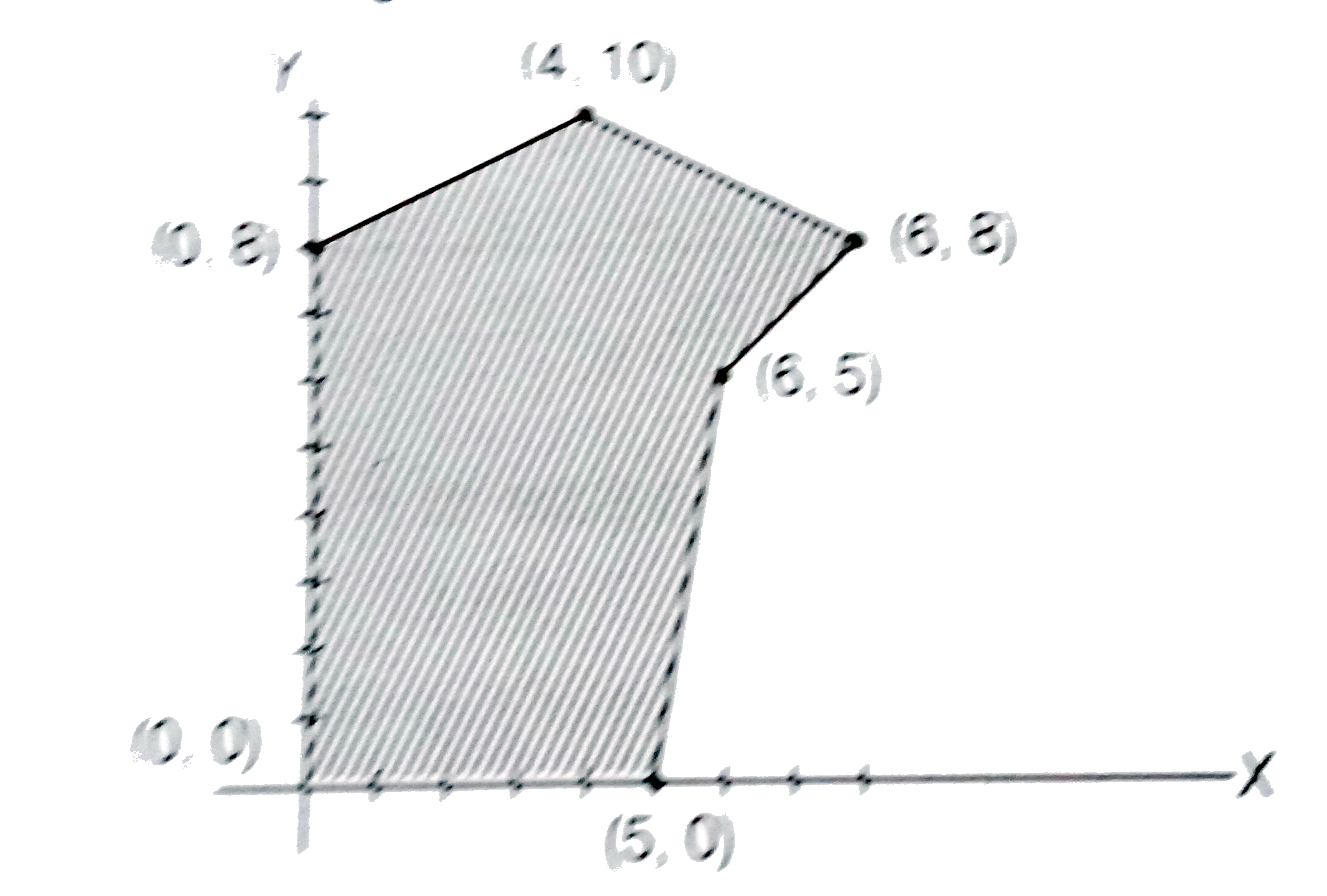
View SolutionIf the objective function for an L.P.P. is Z=3x−4y and the corner points for the bounded feasible region are (0, 0), (5, 0), (6, 5), (6, 8), (4, 10) and (0, 8), then the maximum value of Z occurs at
View SolutionIf the objective function for a L.P.P. is Z=5x+7y and the corner points of the bounded feasible region are (0, 0), (7, 0), (3, 4) and (0, 2), then the maximum value of Z occurs at
View Solution
