Crude oil is being transferred from a full rectangular storage container with dimensions of 4 meters by 9 meters by 10 meters into cylinders transportation contanier that has a diameter of 6 meters. What is the minimum possible length for transportation container that will hold all of the oil?
40π
40π
60π
120π
The correct Answer is:B
To find the minimum possible length of the cylindrical transportation container that will hold all of the crude oil, we can follow these steps:
Step 1: Calculate the volume of the rectangular storage container.
The volume V of a rectangular prism is given by the formula:
V=length×width×height
For the given dimensions of the rectangular container (4 meters by 9 meters by 10 meters):
V=4m×9m×10m=360m3
Step 2: Determine the radius of the cylindrical container.
The diameter of the cylindrical container is given as 6 meters. The radius r is half of the diameter:
r=diameter2=6m2=3m
Step 3: Write the volume formula for the cylindrical container.
The volume V of a cylinder is given by the formula:
V=πr2h
where h is the height (or length) of the cylinder. Substituting the radius:
V=π(3m)2h=9πh
Step 4: Set the volume of the rectangular container equal to the volume of the cylindrical container.
Since the volume of oil remains the same during the transfer, we can set the two volumes equal to each other:
360m3=9πh
Step 5: Solve for h.
To find h, rearrange the equation:
h=3609π
Simplifying this gives:
h=40πm
Conclusion:
The minimum possible length for the cylindrical transportation container that will hold all of the oil is:
40πm
The volume V of a rectangular prism is given by the formula:
V=length×width×height
For the given dimensions of the rectangular container (4 meters by 9 meters by 10 meters):
V=4m×9m×10m=360m3
The diameter of the cylindrical container is given as 6 meters. The radius r is half of the diameter:
r=diameter2=6m2=3m
The volume V of a cylinder is given by the formula:
V=πr2h
where h is the height (or length) of the cylinder. Substituting the radius:
V=π(3m)2h=9πh
Since the volume of oil remains the same during the transfer, we can set the two volumes equal to each other:
360m3=9πh
To find h, rearrange the equation:
h=3609π
Simplifying this gives:
h=40πm
The minimum possible length for the cylindrical transportation container that will hold all of the oil is:
40πm
Topper's Solved these Questions
Similar Questions
Desiree is making apple juice from concentrate. The cylindrical container of concentrate has a diameter of 7 centimmeters ans a height of 12 centimeters. To make the juice, the concentrate must be diluted with water so that the mix is 75 percent water and 25 percent concentrate.
Desiree is going to serve the apple juice in a cylindrical pitcheer with a diameter of 10 centimeters. What is the minimum height of the pitcher, rounded to the nearest centimeter, required for it to hold the apple juice that Desiree made ?
View SolutionIf a wooden right circular cylinder with radius 2 meters and height 6 meters has a cylindrical hole of diameter 2 meters drilled through the center as shown, what is the entire surface area (including the top and bottom faces), in square meters, of the resulting figure ?
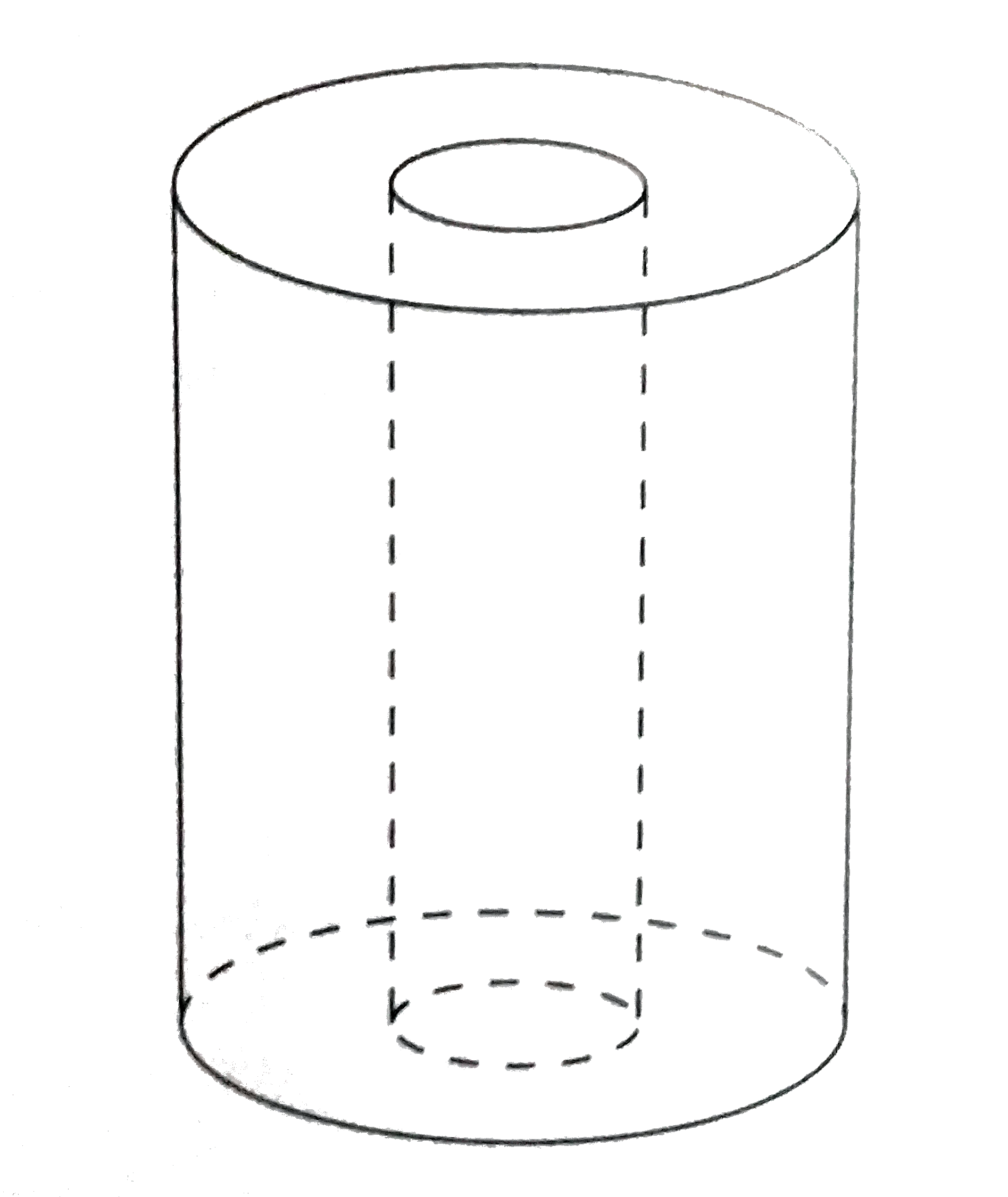
View Solution
Knowledge Check
Milk is poured from a full rectangular container with dimensions 4 inches by 9 inches by 10 inches into cylindrical container with a diameter of 6 inches. Assuming all the milk is transferred without spilage, how many inches high will the milk reach in the cylindrical container?
A40πB60πC24D30A homeowners' association limits the dimensions of the pools that it will allow in a particular subdivision. The bylaws state that permits will only be granted for pools shaped like rectangular prisms, for which the sum of the length of the pool and the perimeter of the vertical side containing the ladder cannot exceed 200 meters. the perimeters of the ladder side is determined using the width and the depth of the pool . IF a pool has a length of 75 meters and its width is 1.5 times its depth, which of the following shows the allowable depth a, in meters, of the pool?
A0<a<6212B0<a≤50C0<a≤3114D0<a≤25h(t)=−4.9t2+68.6t
The function above gives the height of a model rocket, in meters, t seconds after it is launched from ground level. What is the maximum height, to the nearest meter, attained by the model rocket?A90B120C180D240
Figure shows (only cross section) a wooden cylinder C with a mass m of 0.25kg,a radius R and a length l perpenducular to the plane of paper of 0.1meter with N=10 where N is number of turns of wire loop contains the axis of the cylinder the least current through the loop is P2A that will prevent the cylinder from moving down a plane whose surface is inclined at angle θ to the horizontal, in the presence of a vertical field of magnetic induction 0.5weber/meter2, if the planer of the windings is parallel to the inclinded plane?(bottom most point of cylinder does not slip)then find value of P.
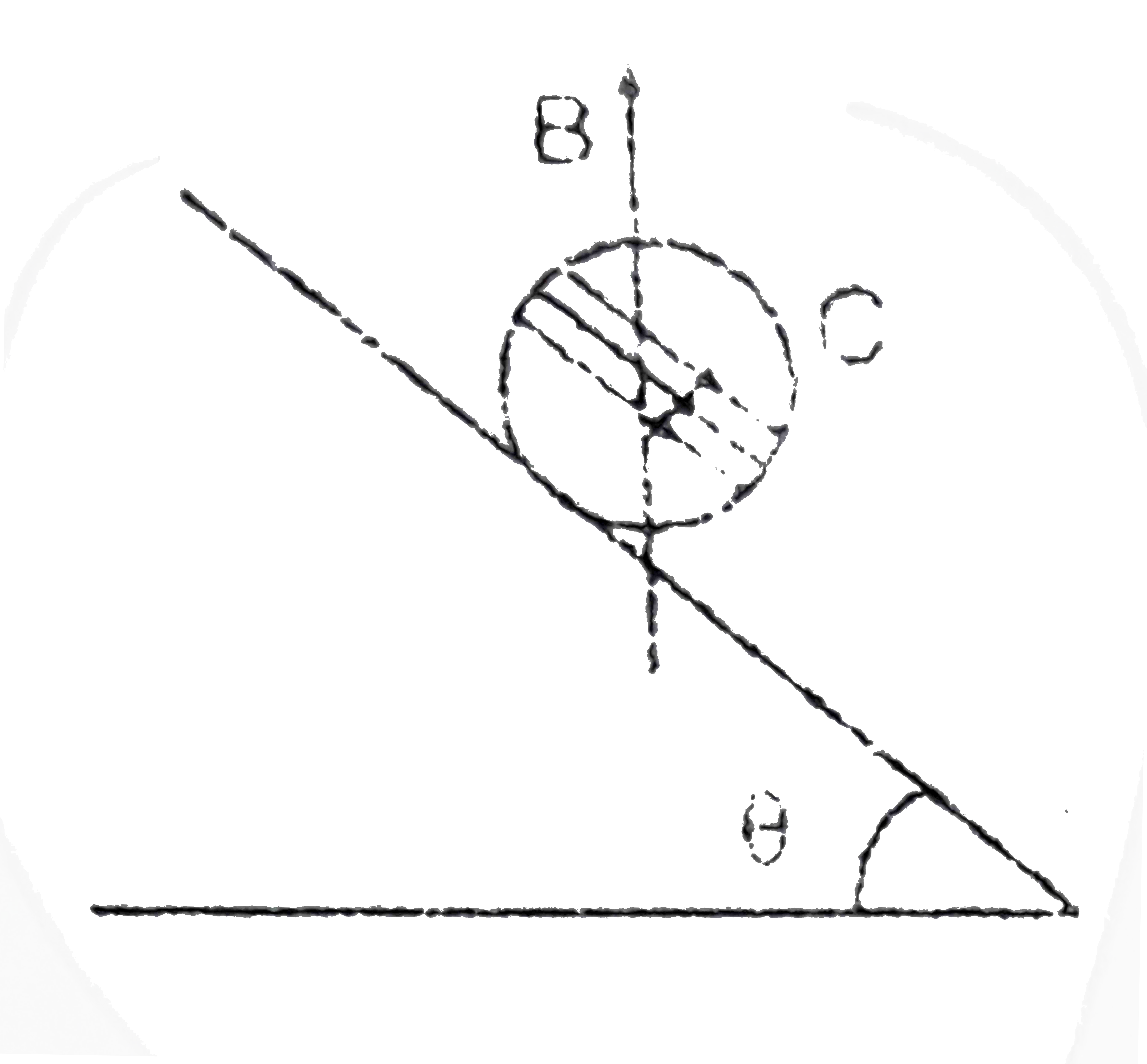
View SolutionA soft drink is available in two packs – (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
View SolutionA soft drink is available in two packs - (i) a tin can with a rectangular base of length 5cm and width 4cm, having a height of 15cm and (ii) a plastic cylinder with circular base of diameter 7cm and height 10cm. Which container has greater capacity and by how much?
View SolutionA soft drink is available in two packs - (i) a tin can with a rectangular base of length 5cm and width 4cm, having a height of 15cm and (ii) a plastic cylinder with circular base of diameter 7cm and height 10cm. Which container has greater capacity and by how much?
View SolutionA square field measures 10 meters by 10 meters. Ten students each mark off a randomly selected region of the field, each region is square and has side lengths of 1 meter, and no two regions overlap. The students count the earthworms contained in the soil to a depth of 5 centimeters beneath the ground’s surface in each region. The results are shown in the table below.
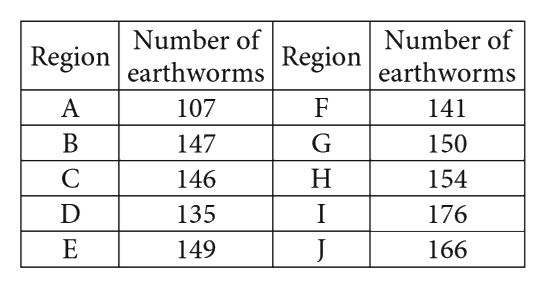
Which of the following is a reasonable approximation of the number of earthworms to a depth of 5 centimeters beneath the ground’s surface in the entire field?
View Solution