D is a point on the base BC of $Δ A B C . A D$ is produced upto E such that DE = AD. Prove that:
area of $Δ B C E = area of Δ A B C$

Video Solution

Answer

Step by step video, text & image solution for D is a point on the base BC of Delta ABC.AD is produced upto E such that DE = AD. Prove that: area of Delta BCE = " area of " Delta ABC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos

Knowledge Check

If D is a Point on the side BC of a $Δ A B C$ such that AD bisects $∠ B A C$ . Then
ABD=CD
B $B A > B D$
C $B D > B A$
D $C D < C A$
ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of $Δ A D C$ to the area of $Δ A B C$ ?
A $3 / 2$
B $2 / 3$
C $3 / 5$
D $2 / 5$

If D is a point on the side AB of $Δ A B C$ such that $A D : B D = 3 : 2 and E$ is a point on BC such that $D E ∣ ∣ A C$ , find the ratio of the areas of $Δ A B C and Δ D B E$

View Solution
In a triangle ABC, D is mid-point of BC; AD is produced upto E so that DE = AD Prove that: (i) $△ A B D and △ E C D$ are congruent. (ii) AB = EC. (ii) AB is parallel to EC
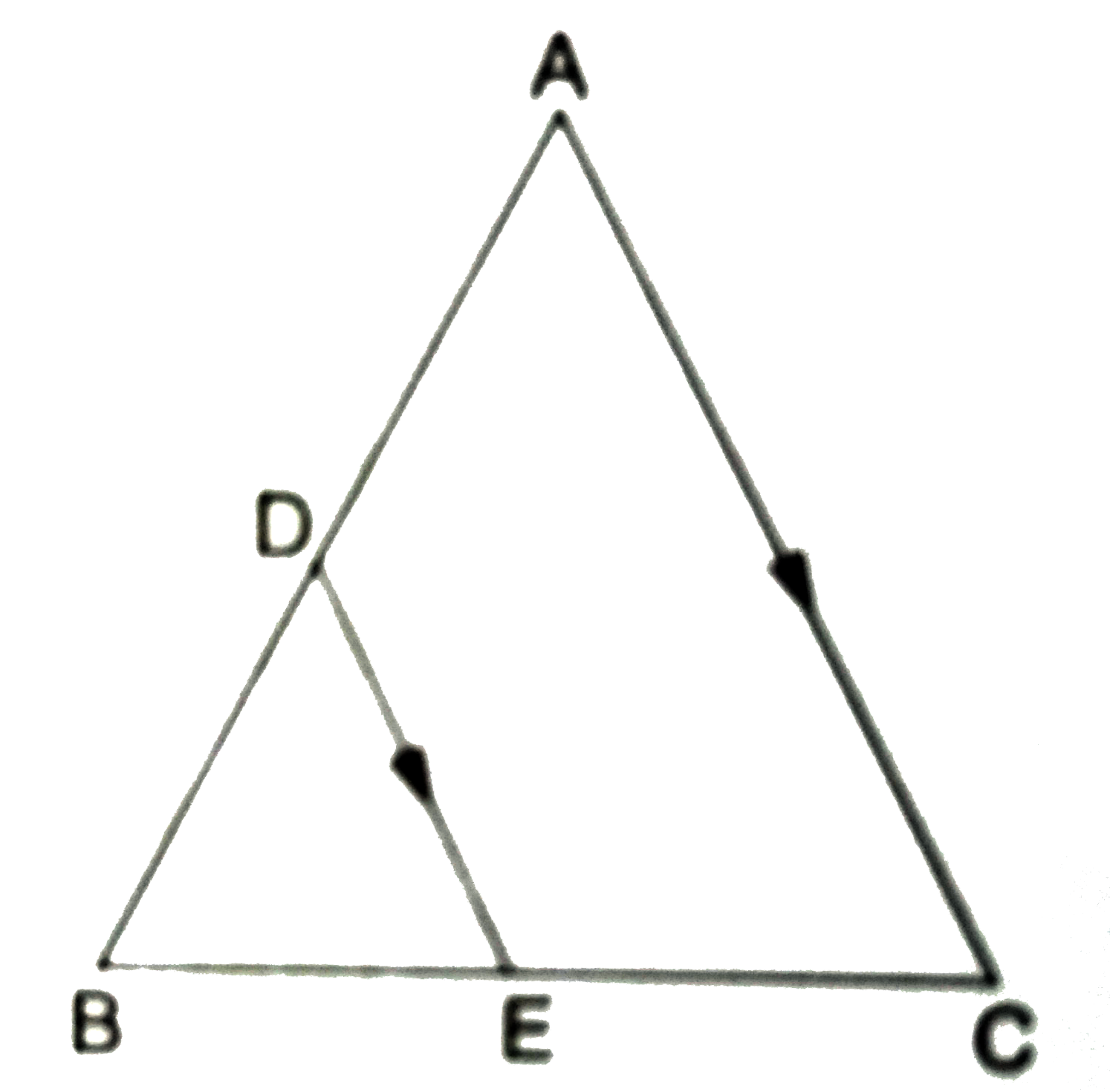
View Solution
In the adjoining figure, D is the mid-point of side AB of $Δ A B C$ and P be any point on side BC. If $C Q ∣ ∣ P D$ , then prove that:
area of $Δ B P Q = \frac{1}{2} \times area of Δ A B C$

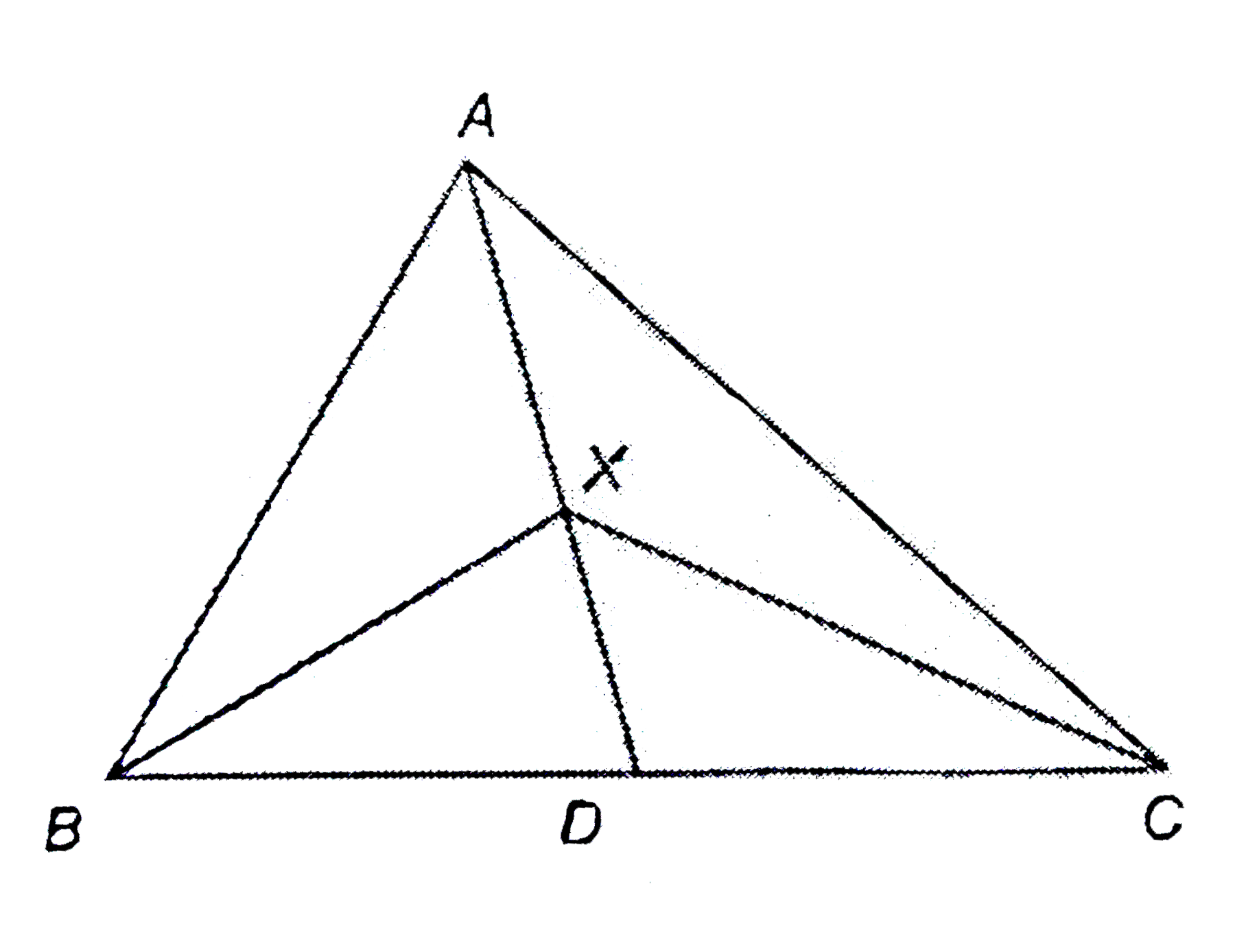
View Solution
In the adjoining figure, AD is the median of $Δ A B C$ and X be any point on side AD. Prove that:
area $(Δ A B X) = area (Δ A C X)$

View Solution
$Δ A B C and Δ D B C$ are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of $Δ A B C = area of Δ D B C$
Prove that BC bisects the line segment AD.
View Solution
If $D$ is any point on the base $B C$ produced, of an isosceles triangle $A B C,$ prove that $A D > A B$ .
View Solution

NAGEEN PRAKASHAN-AREA OF PARALLELOGRAMS AND TRIANGLES-Exercise

In the adjoning figure, ABCD is a parallelogram. Prove that : area of ...
08:29
In a quadrilateral ABCD, AM and CN are perpendiculars from the vertice...
01:02
In the adjoining figure, ABCD is a quadrilateral in which AD ||BC. AC ...
01:11
D is a point on the base BC of Delta ABC.AD is produced upto E such th...
03:21
In the adjoining figure, D is the mid-point of side AB of Delta ABC an...
03:01
In a A B C ,\ E is the mid-point of median A Ddot Show that a r\ (...
02:49
In parallelogram ABCD, P is a point on side AB and Q is a point on sid...
01:50
In the given figure, M and N are the mid-points of the sides DC and AB...
00:57
ABCD and BCFE are parallelgorams. If area of triangle EBC = 480 cm^(2)...
02:02
The given figure shows a pentagon ABCDE.EG drawn parallel to DA meets ...
06:56
In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove...
01:15
The following figure shows two paralelograms ABCD and ABEF prove that ...
01:01
The side AB of a parallelogram ABCD is produced to any point E. A line...
01:47
A point E is taken on the side BC of a parallelogram ABCD. AE and DC a...
05:45
In the following figure, AP||PS||QR and PQ||DB||SR, prove that area of...
02:08
O is any point on the diagonal B D of the parallelogram A B C Ddot Pro...
02:45
D is the mid-point of side AB of the triangle ABC.E is the mid-point o...
01:41
In triangle ABC,E and F are the mid-point of sides AB and AC respectiv...
01:58
ABCD is a parallelogram. P and Q are the mid-point of sides AB and AD ...
01:04
In the given figure, squares ABDE and AFGC are drawn on the side AB an...
08:26

Home
Ask Doubt
Profile

D is a point on the base BC of ΔABC.AD is produced upto E such that DE = AD. Prove that: area of ΔBCE= area of ΔABC

Topper's Solved these Questions

Similar Questions

Knowledge Check

If D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then

ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of ΔADC to the area of ΔABC ?

NAGEEN PRAKASHAN-AREA OF PARALLELOGRAMS AND TRIANGLES-Exercise

D is a point on the base BC of $Δ A B C . A D$ is produced upto E such that DE = AD. Prove that:
area of $Δ B C E = area of Δ A B C$

If D is a Point on the side BC of a $Δ A B C$ such that AD bisects $∠ B A C$ . Then

ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of $Δ A D C$ to the area of $Δ A B C$ ?