In a ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
Step by step video, text & image solution for In a A B C ,\ E is the mid-point of median A Ddot Show that a r\ ( B E D)=1/4a r\ ( A B C) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of â–³BED=14areaofâ–³ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(â–³BED)=14ar(â–³ABC).
View SolutionIf AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid-point of median AD, prove that ar (BGC)=2ar ( AGC)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)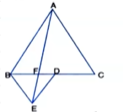
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
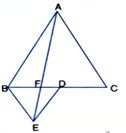View SolutionIn ABC, E is the mid-point of median AD such that BE produced meets AC at F. If AC=10.5 CM, then AF= 3cm (b) 3.5cm (c) 2.5cm (d) 5cm
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View Solution