ΔABCandΔCDE are two equilateral triangles such that D is the mid -point of BC . The ratio of the areas of ΔCDEandΔABC is 1 : k then k =
The correct Answer is:∴k=4.
To solve the problem, we need to find the value of k in the ratio of the areas of two equilateral triangles ΔABC and ΔCDE, given that D is the midpoint of BC.
1. Understanding the Triangles:
- We have two equilateral triangles, ΔABC and ΔCDE.
- Point D is the midpoint of side BC of triangle ABC.
2. Identifying Corresponding Sides:
- Since D is the midpoint of BC, we can denote the length of side BC as a. Therefore, BD=CD=a2.
3. Using the Property of Similar Triangles:
- Since both triangles are equilateral, they are similar. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
4. Setting Up the Ratio of Areas:
- The area of triangle CDE can be expressed in terms of the side CD, which is a2.
- The area of triangle ABC is based on the side a.
5. Calculating the Areas:
- The area of triangle ABC is given by the formula:
AreaABC=√34a2
- The area of triangle CDE is given by:
AreaCDE=√34(a2)2=√34⋅a24=√316a2
6. Finding the Ratio of Areas:
- Now, we can find the ratio of the areas:
AreaCDEAreaABC=√316a2√34a2=11614=14
7. Expressing in Terms of k:
- We are given that the ratio of the areas of ΔCDE to ΔABC is 1:k.
- From our calculation, we found that:
AreaCDEAreaABC=14
- Therefore, we can write:
1:k=1:4
- This implies that k=4.
Final Answer:
Thus, the value of k is 4.
- We have two equilateral triangles, ΔABC and ΔCDE.
- Point D is the midpoint of side BC of triangle ABC.
- Since D is the midpoint of BC, we can denote the length of side BC as a. Therefore, BD=CD=a2.
- Since both triangles are equilateral, they are similar. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- The area of triangle CDE can be expressed in terms of the side CD, which is a2.
- The area of triangle ABC is based on the side a.
- The area of triangle ABC is given by the formula:
AreaABC=√34a2
- The area of triangle CDE is given by:
AreaCDE=√34(a2)2=√34⋅a24=√316a2
- Now, we can find the ratio of the areas:
AreaCDEAreaABC=√316a2√34a2=11614=14
- We are given that the ratio of the areas of ΔCDE to ΔABC is 1:k.
- From our calculation, we found that:
AreaCDEAreaABC=14
- Therefore, we can write:
1:k=1:4
- This implies that k=4.
Thus, the value of k is 4.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner15videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)7videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
ΔPOR and ΔQST are two equilateral triangles such that T is the mid-point of QR. Find the ratio of areas of ΔPOR and ΔQST.
 View Solution
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
View Solution
Knowledge Check
- Question 1 - Select One
ΔPQR and ΔQST are two equilateral triangles such that T is the mid-point of QR. Find the ratio of the areas of ΔPQR and ΔQST.
 A1:1B1:2C2:1D4:1
A1:1B1:2C2:1D4:1 - Question 2 - Select One
ABC and BDE are two equilateral triangle such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
A2:1B1:2C4:1D1:4 - Question 3 - Select One
ABC and BDF are two equilateral triangle such that D is the mid - point of BC. Ratio of the areas of triangles ABC and BDF is .
A2:1B1:2C4:1D1:4
Tick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
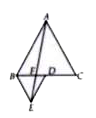
ar(ΔBDE) = 1/4 ar(ΔABC)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
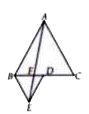
ar(ΔBDE) = 1/2 ar(ΔBAE)View SolutionABC and BDE are two equilateral trainales, such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is :
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View Solution

