Tick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4
∠ABC~∠BDE
because both the triangles are equilateral triangle.
area(ABC)area(BDC)=(BCBD)2=22=4
so they are in 4:1 ratio
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Exercise 6.13videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Exercise 6.210videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES14videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.28videos
SURFACE AREAS AND VOLUMES
Similar Questions
ABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
View SolutionΔABCandΔCDE are two equilateral triangles such that D is the mid -point of BC . The ratio of the areas of ΔCDEandΔABC is 1 : k then k =
View Solution
Knowledge Check
- Question 1 - Select One
ABC and BDE are two equilateral triangle such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
A2:1B1:2C4:1D1:4 - Question 2 - Select One
ABC and BDE are two equilateral trainales, such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is :
A1:4B1:2C2:1D4:1 - Question 3 - Select One
ABC and BDF are two equilateral triangle such that D is the mid - point of BC. Ratio of the areas of triangles ABC and BDF is .
A2:1B1:2C4:1D1:4
Tick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid point of BC Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2:3 (B) 4:9 (C) 81:16 (D) 16:81View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
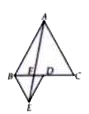
ar(ΔBDE) = 1/2 ar(ΔBAE)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
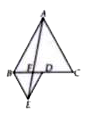
ar(ΔABC) = 2 ar(ΔBEC)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
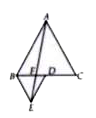
ar(ΔBDE) = 1/4 ar(ΔABC)View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View Solution

