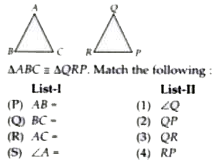
$Δ A B C ≅ Δ Q R P$ . Match the following :
$\begin{matrix} (P) & A B = & (1) & ∠ Q (Q) & B C = & (2) & Q P (R) & A C = & (3) & Q R (S) & ∠ A = & (4) & R P \end{matrix}$

P-1, Q-2, R-3, S-4

P-3, Q-2, R-4, S-1

P-3, Q-4, R-2, S-1

P-2, Q-3, R-4, S-1

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Let $Δ A B C ~ Δ P Q R and \frac{a r (Δ A B C)}{a r (Δ P Q R)} = \frac{4}{25}$ . If $A B = 12 c m, B C = 8 c m and A C = 10 c m$ then QR is equal to
Aa)15
Bb)18
Cc)25
Dd)20
In $Δ A B C, ∠ C = ∠ A, B C = 4 c m and A C = 5 c m .$ Then, AB = ?
A4 cm
B5 cm
C5 cm
D2.5 cm
In $Δ A B C$ , if $∠ A : ∠ B : ∠ C = 1 : 2 : 3$ , then what is $B C : C A : A B ?$
A $1 : 2 : 3$
B $1 : \sqrt{3} : 2$
C $2 : \sqrt{3} : 1$
D $\sqrt{3} : 1 : 2$