In ΔABC, bisector of ∠A intersects BC at D. If AB = 4 cm, AC = 3 cm and ∠A=60∘, then find the length of AD-
12√35
12√57
15√37
12√37
To find the length of AD in triangle ABC where the angle bisector of angle A intersects BC at D, we can follow these steps:
Step 1: Understand the triangle and given values
We have triangle ABC with:
- AB = 4 cm
- AC = 3 cm
- Angle A = 60 degrees
Step 2: Use the area formula for triangle ABC
The area of triangle ABC can be calculated using the formula:
Area=12×AB×AC×sin(A)
Substituting the values:
Area=12×4×3×sin(60∘)
Since sin(60∘)=√32, we have:
Area=12×4×3×√32=6√3 cm2
Step 3: Use the area of triangle ABD and ACD
The area of triangle ABD can also be expressed as:
AreaABD=12×AB×AD×sin(30∘)
And the area of triangle ACD can be expressed as:
AreaACD=12×AC×AD×sin(30∘)
Since sin(30∘)=12, we can write:
AreaABD=12×4×AD×12=AD cm2
AreaACD=12×3×AD×12=34AD cm2
Step 4: Relate the areas
The total area of triangle ABC is the sum of the areas of triangles ABD and ACD:
6√3=AD+34AD
This simplifies to:
6√3=74AD
Step 5: Solve for AD
To find AD, multiply both sides by 47:
AD=6√3×47=24√37 cm
Final Answer
Thus, the length of AD is:
AD=24√37 cm
We have triangle ABC with:
- AB = 4 cm
- AC = 3 cm
- Angle A = 60 degrees
The area of triangle ABC can be calculated using the formula:
Area=12×AB×AC×sin(A)
Substituting the values:
Area=12×4×3×sin(60∘)
Since sin(60∘)=√32, we have:
Area=12×4×3×√32=6√3 cm2
The area of triangle ABD can also be expressed as:
AreaABD=12×AB×AD×sin(30∘)
And the area of triangle ACD can be expressed as:
AreaACD=12×AC×AD×sin(30∘)
Since sin(30∘)=12, we can write:
AreaABD=12×4×AD×12=AD cm2
AreaACD=12×3×AD×12=34AD cm2
The total area of triangle ABC is the sum of the areas of triangles ABD and ACD:
6√3=AD+34AD
This simplifies to:
6√3=74AD
To find AD, multiply both sides by 47:
AD=6√3×47=24√37 cm
Thus, the length of AD is:
AD=24√37 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC,AB=5cm,AC=5cmandangleA=50∘, then ∠B=
A35∘B65∘C80∘D40∘In the figure AD is the external bisector of ∠EAC, intersects BC produced to D. IF AB=12cm,AC=8cmandBC=4cm, find CD :
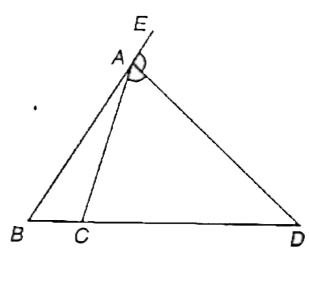 A10 cmB6 cmC8 cmD9 cm
A10 cmB6 cmC8 cmD9 cmLet ABC be a triangle with ∠B=90∘. Let AD be the bisector of ∠A with D on BC. Supose AC = 6 cm and the area of the triangle ADC is 10 cm2 . Then the length of BD in cm is equal to
A35B310C53D103
In ΔABC , ∠A is right - angled . If AB= 1 cm , AC =3 cm and BC = √10 cm , then find the values of cos B and sin C.
View SolutionIn ΔABC, angle bisector of ∠A intersect BC at D and intersects circumcircle of triangle at E then.
View SolutionIf in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
View SolutionIn a ΔABC it is given AD is internal bisector of ∠A . If BD=4cm,DC=5cmandAB=6cm, then AC =?
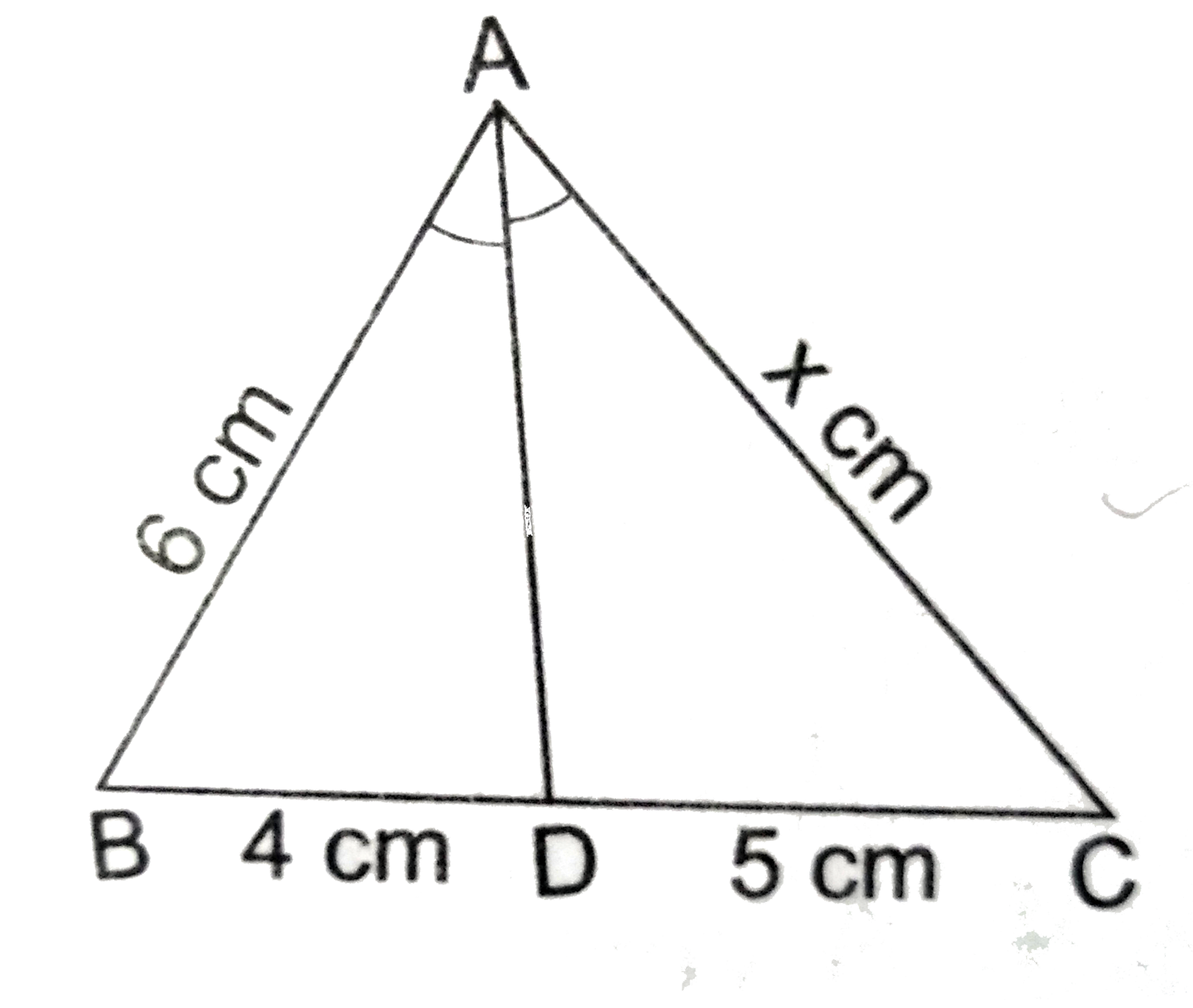
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View Solution
