Determine whether the function has y-symmetry or origin symmetry : Solution in Bengali
(i) , hence the function has origin symmetry
(ii) hence the function has origin symmetry
(iii)
= f(x)
Hence the function has y-symmetry.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.4
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.5
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.2
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
The graph of functions are given in the following fingure. Discuss the symmetry.
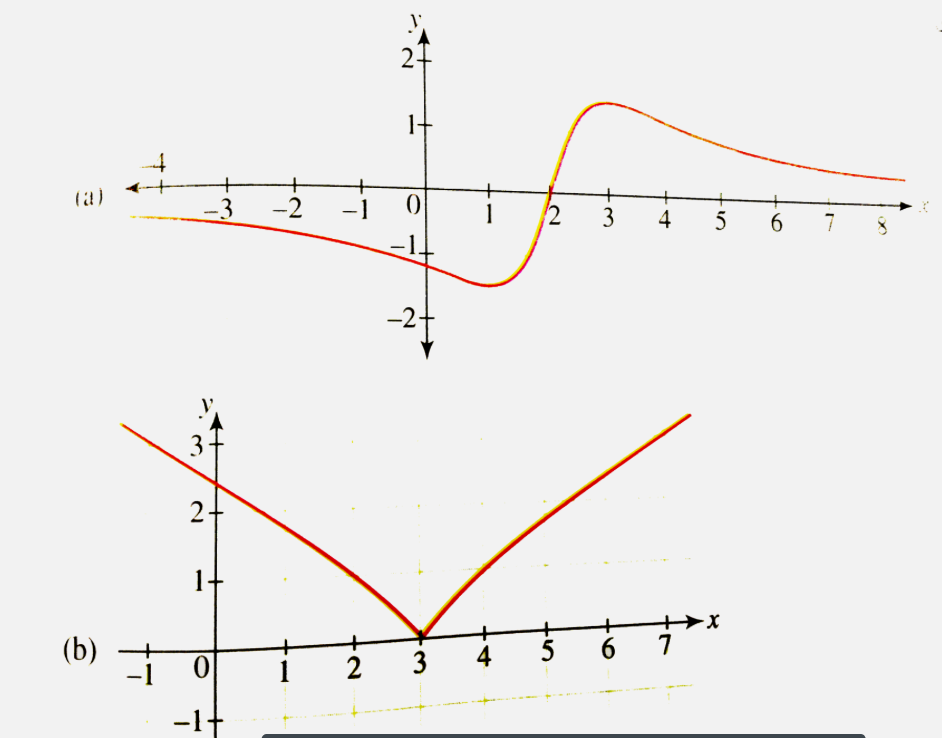
View SolutionCheck weather the following function/functions is/are periodic or not? Find the period in case the function is periodic.
View SolutionConsider the graph of y = f(x) as shown in the following figure.
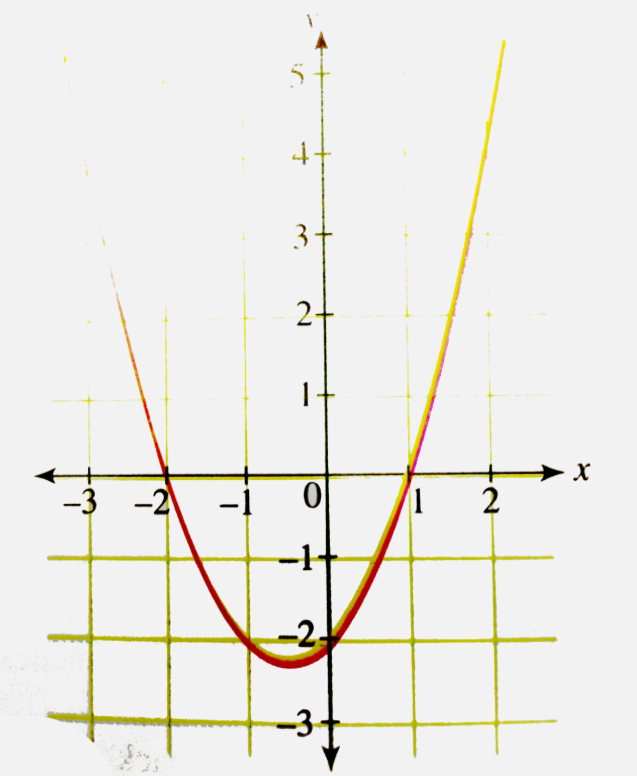
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionConsider that the graph of y=f(x) is symmetrie about the lines x=2 and x=4 then the period of f(x) is
View SolutionDoes the fraph of the function f(x)=x2−3 have y - axis symmetry?
View SolutionDoes the graph of the function f(x)=1/x3 have origin symmetry?
View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) f(x)=x2sinx (ii)f(x)=log(x+√1+x2)
(iii)f(x)=ex+e−x2 (iv)f(x)={0, If x is rational 1, If x is irrational
View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) f(x)=x2sinx (ii)f(x)=log(1−x1+x)
(iii)f(x)=xex−1+x2+1
View SolutionDetermine whether the function f(x)=x(ex−1ex+1) is even or odd
View SolutionExamine whether the function are even or odd or none.
f(x)=xex−1+x2+1
View SolutionDoes the graph of the function f(x)=x2−3 have y - axis symmetry?
View SolutionDoes the graph of the function f(x)=1/x3 have origin symmetry?
View SolutionCheck whether the function has (have) y-symmetry or origin symmetry: f(x)=x2sinx.
View SolutionDetermine whether the function has y-symmetry or origin symmetry : f(x)=xex−1+x2+1
View Solution
