Does the fraph of the function f(x)=x2−3 have y - axis symmetry?
We need to check if f(a) = f(-a).
f(−a)=(−a)2−3=a2−3=f(a)
Therefore, the function f(x)=x2−3 must have y - axis symmetry.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank30videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
For the function f(x,y)=2x4−3x2y+y2 has
Amaximum at (0,0)Bminimum at (0,0)Cneither maxima or minima at (0,0)Ddoubtful case at (0,0) always . - Question 2 - Select One
If the graph of the function f(x)=ax−1xn(ax+1) is symmetric about y - axis, then n is equal to :
Aa.−13Bb. 14Cc. 2/3Dd. 2 - Question 3 - Select One or More
If the graph of the function f(x)=ax−1xn(ax+1) is symmetric about y-axis then n is equal to
A1/5B1/3C1/4D−1/3
Consider the following graph of the function y=f(x). Which of the following is/are correct? fig. (lim)x→1f(x) does not exist. (lim)x→2f(x) does not exist. (lim)x→3f(x)=3
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
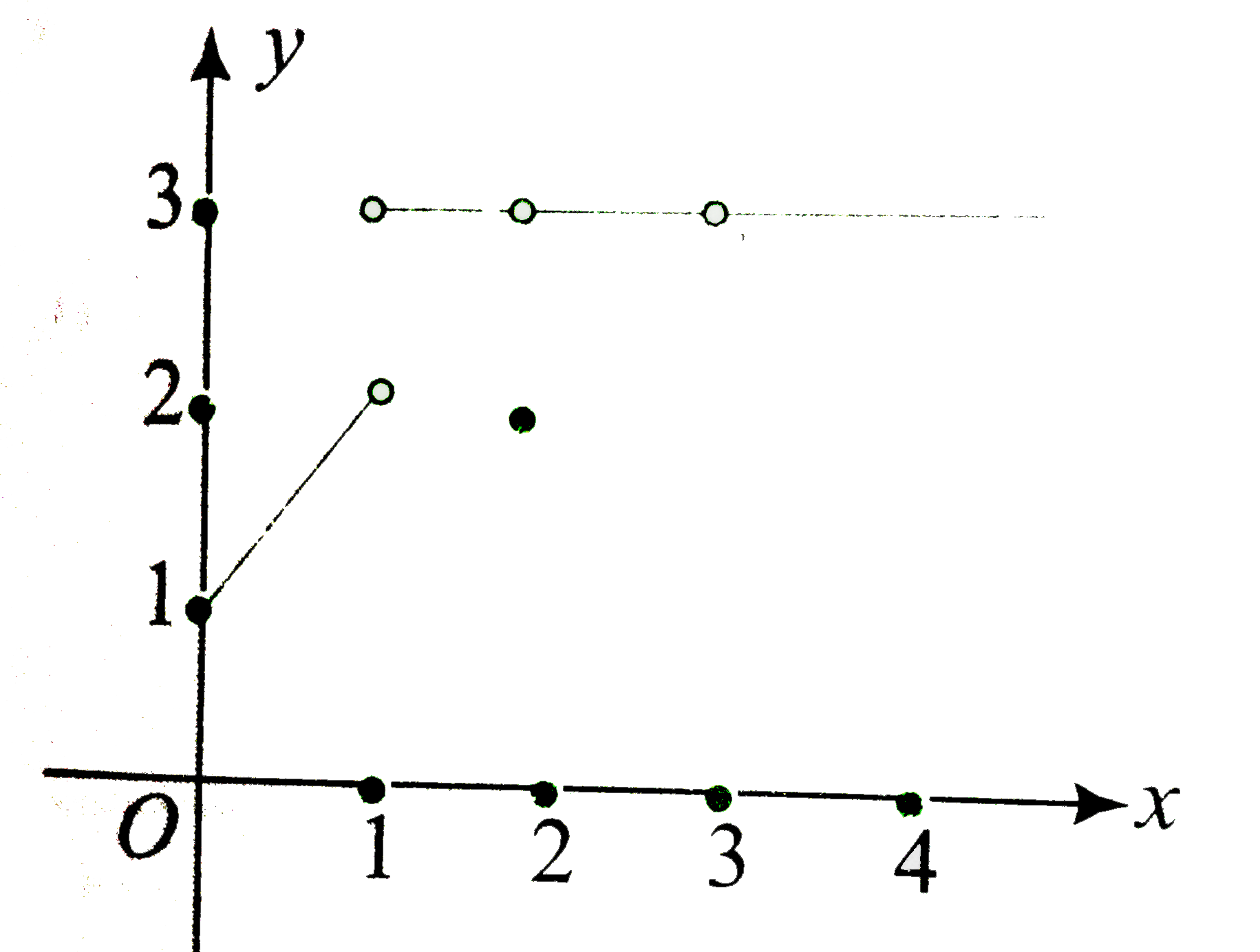
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) f(x)=x2sinx (ii)f(x)=log(1−x1+x)
(iii)f(x)=xex−1+x2+1View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1 Then draw the graph of the function y=f(x),y=f(|x|),y=|f(x)|,andy=|f(x)|.
View SolutionWhich of the following functions has (have) y-symmetry or origin symmetry?
(i) f(x)=x2sinx (ii)f(x)=log(x+√1+x2)
(iii)f(x)=ex+e−x2 (iv)f(x)={0, If x is rational 1, If x is irrationalView Solution

