Diagonal PR and QS of quadrilateral PQRS intersects at T such that PT= TR and PS= QR, show that ar (ΔPTS)= ar (ΔRTQ)
To prove that the area of triangle PTS is equal to the area of triangle RTQ, we will follow these steps:
1. Identify the Given Information:
- Diagonals PR and QS intersect at point T.
- It is given that PT=TR and PS=QR.
2. Draw the Quadrilateral:
- Draw quadrilateral PQRS with diagonals PR and QS intersecting at point T.
3. Label the Angles:
- Identify and label angles ∠PTS and ∠QTR. Since T is the intersection point of the diagonals, these angles are vertically opposite angles.
4. Use the Property of Vertically Opposite Angles:
- State that ∠PTS=∠QTR because they are vertically opposite angles.
5. Apply the Given Lengths:
- From the problem, we know PT=TR (let's denote this length as x) and PS=QR (let's denote this length as y).
6. Establish Triangle Congruence:
- We can now use the Side-Angle-Side (SAS) congruence criterion:
- Side PT=TR (given)
- Angle PTS=QTR (from step 4)
- Side PS=QR (given)
- Therefore, triangles PTS and RTQ are congruent by SAS.
7. Conclude Equal Areas:
- Since triangles PTS and RTQ are congruent, their areas are equal:
Area(ΔPTS)=Area(ΔRTQ)
Final Statement:
Thus, we have shown that Area(ΔPTS)=Area(ΔRTQ).
---
- Diagonals PR and QS intersect at point T.
- It is given that PT=TR and PS=QR.
- Draw quadrilateral PQRS with diagonals PR and QS intersecting at point T.
- Identify and label angles ∠PTS and ∠QTR. Since T is the intersection point of the diagonals, these angles are vertically opposite angles.
- State that ∠PTS=∠QTR because they are vertically opposite angles.
- From the problem, we know PT=TR (let's denote this length as x) and PS=QR (let's denote this length as y).
- We can now use the Side-Angle-Side (SAS) congruence criterion:
- Side PT=TR (given)
- Angle PTS=QTR (from step 4)
- Side PS=QR (given)
- Therefore, triangles PTS and RTQ are congruent by SAS.
- Since triangles PTS and RTQ are congruent, their areas are equal:
Area(ΔPTS)=Area(ΔRTQ)
Thus, we have shown that Area(ΔPTS)=Area(ΔRTQ).
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-D5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PRACTICE TEST2videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)View SolutionIn the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar(ΔDCB) = ar(ΔACB)View Solution
Knowledge Check
- Question 1 - Select One
If PS is median of the triangle PQR, then ar(ΔPQS): ar(ΔQRP) is
 A1 : 1B2 : 1C1 : 2DCan't be determined
A1 : 1B2 : 1C1 : 2DCan't be determined
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar (ΔPOA)= ar (ΔQOC).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
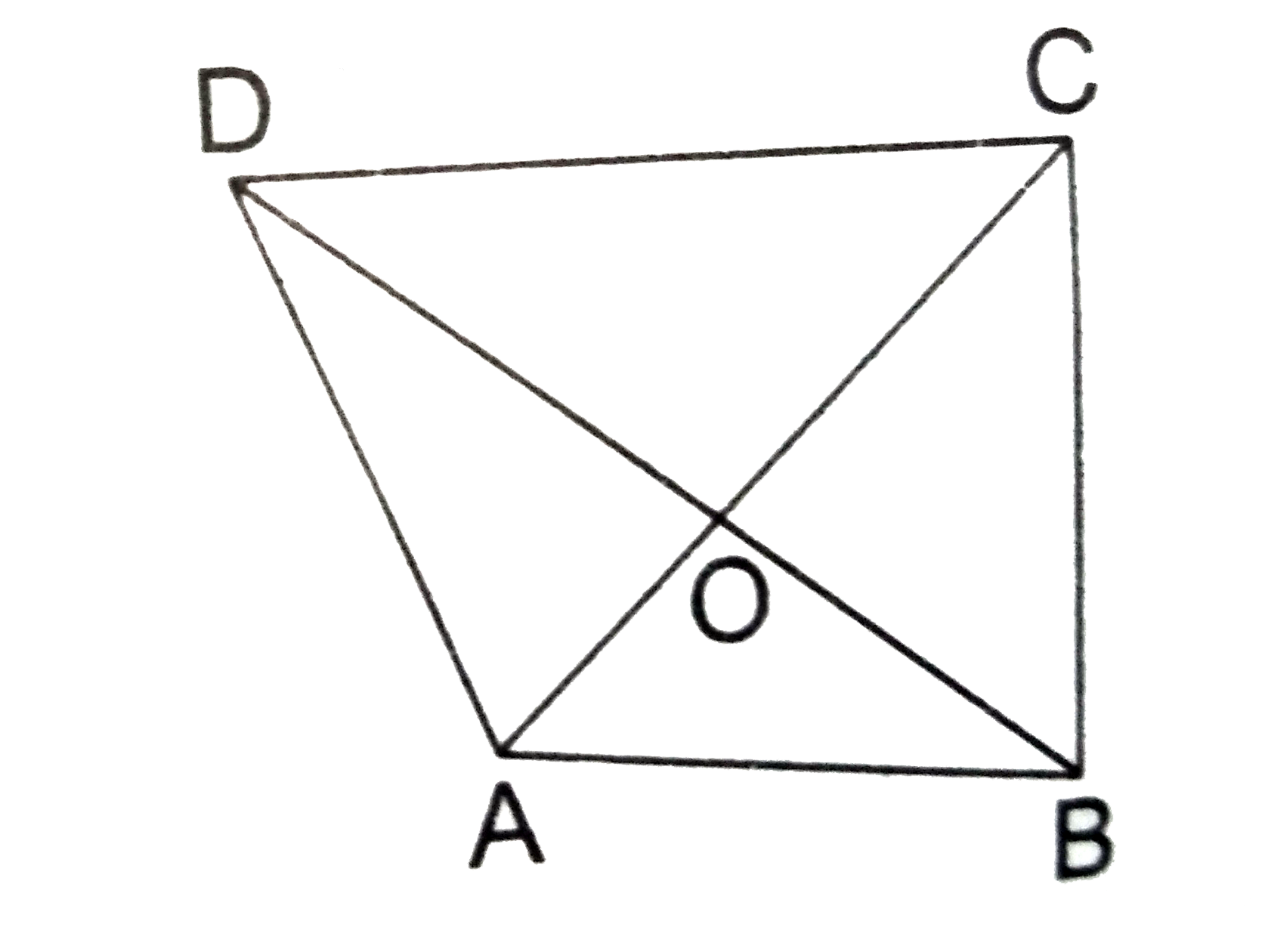
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
 View Solution
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
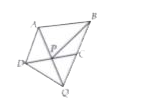
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
 View Solution
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
 View Solution
View Solution

