In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
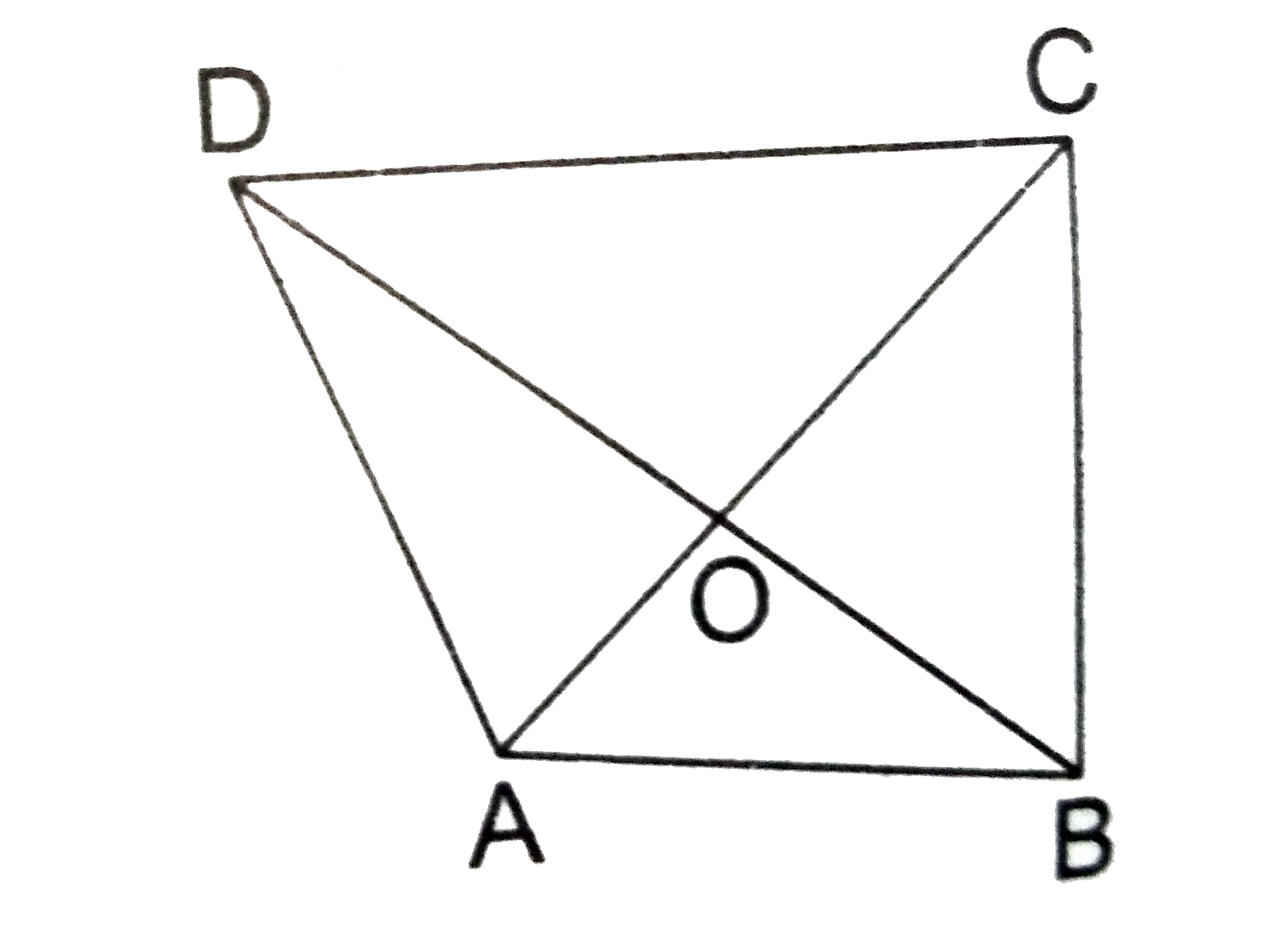
CO is a median of △BCD⇒ar(△COD)=ar(△COB).
AO is a median of △ABD⇒ar(△AOD)=ar(△AOB).
∴ar(△COD)+ar(△AOD)=ar(△COB)+ar(△AOB).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
Diagonals AC and BD of a quadrilateral intersect at O. It AO:OC=1:2=BO:ODandAB=16cm then DC is
A16cmB8cmC4cmD32cm
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)View SolutionIn the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar(ΔDCB) = ar(ΔACB)View SolutionIn Fig 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.If AB=CD , then show that
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionThe diagonals of quadrilateral ABCD, AC and BD intersects at O. Prove that if BO = OD then the triangles ABC and ADC are equal in area.
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that

DA I I CB or ABCD is a parallelogram.View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View Solution