Question

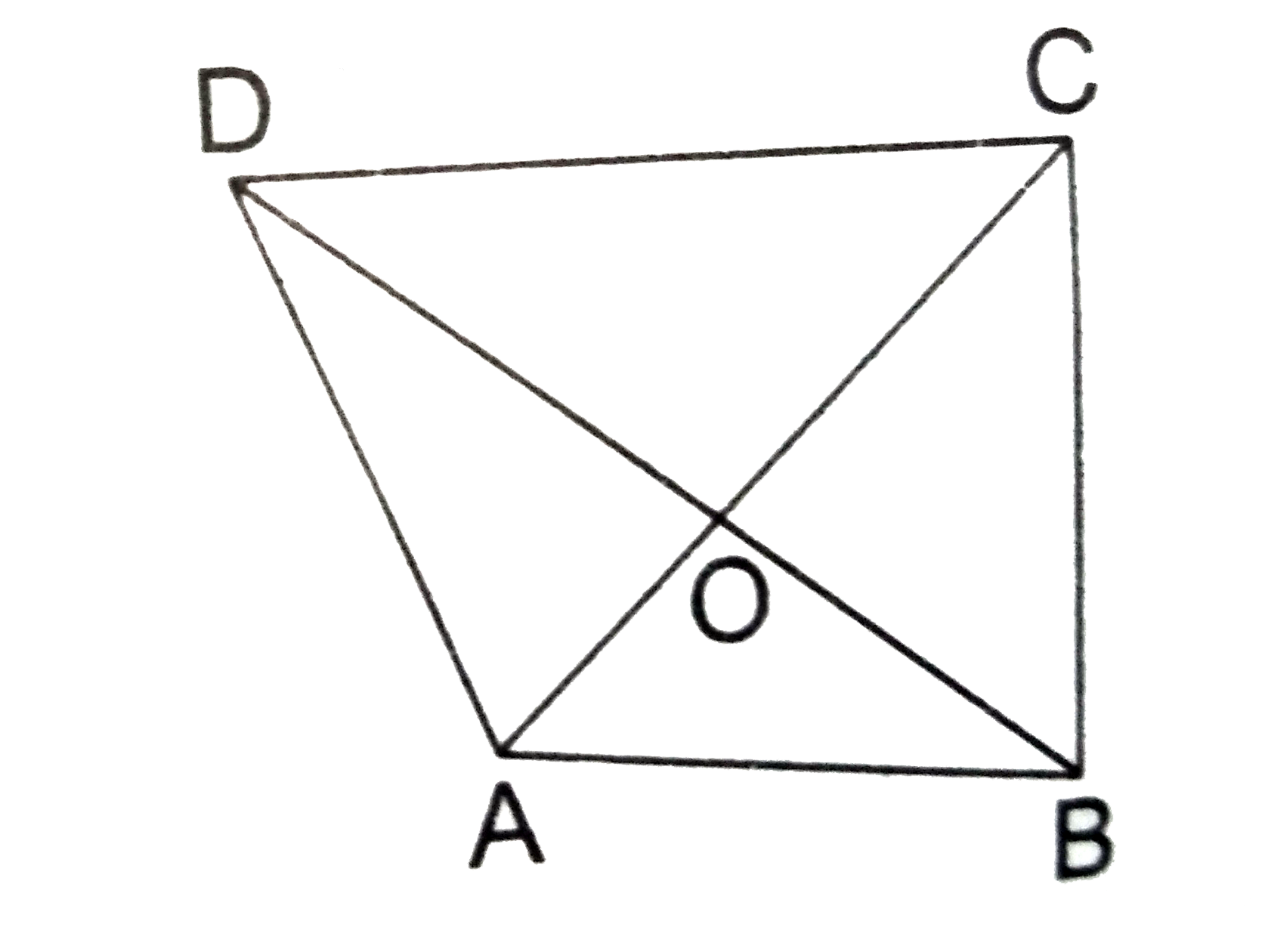
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that${\displaystyle ar\left(AOD\right)=ar\left(BOC\right)\stackrel{.}{}}$Prove that ABCD is a trapezium.

Explanation

To prove that quadrilateral ABCD is a trapezium given that the area of triangle AOD is equal to the area of triangle BOC, we can follow these steps:

Step 1: Understand the Given Information
We know that diagonals AC and BD of quadrilateral ABCD intersect at point O such that:
\( \text{Area of } \triangle AOD = \text{Area of } \triangle BOC \)

Step 2: Add the Areas
We can add the areas of triangles AOD and BOC:
\( \text{Area of } \triangle AOD + \text{Area of } \triangle BOC = 2 \times \text{Area of } \triangle BOC \)
This means:
\( \text{Area of } \triangle AOD + \text{Area of } \triangle BOC = \text{Area of } \triangle ACD + \text{Area of } \triangle BDC \)

Step 3: Identify the Triangles
From the previous step, we can identify that:
- The area of triangle ACD is equal to the area of triangle BDC since both are equal to the sum of the areas of triangles AOD and BOC.

Step 4: Use the Area Property
According to the theorem, if two triangles have the same base and equal areas, they lie between the same parallels. Here, triangles ACD and BDC share the base DC.

Step 5: Conclude Parallelism
Since triangles ACD and BDC have the same base DC and equal areas, it follows that:
- Line AB is parallel to line DC.

Step 6: Define Trapezium
A trapezium (or trapezoid) is defined as a quadrilateral with at least one pair of parallel sides. Since we have established that AB is parallel to DC, we conclude that:
- Quadrilateral ABCD is a trapezium.

Final Conclusion
Thus, we have proved that quadrilateral ABCD is a trapezium.

---