Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60∘. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
In order to draw the pair of tangents, we follow the following steps.
Steps of construction
1. Take a point O on the plane of the paper and draw a circle of radius OA=4 cm.
2. Produce OA to B such that OA=AB=4 cm.
3. Taking A as the centre draw a circle of radius AO=AB=4 cm.
Suppose it cuts the circle drawn in step 1 at P and Q.
4. Join BP and BQ to get desired tangents.
Justification In ΔOAP, we have
OA=OP=4cm (∴ Radius )
Also, AP=4cm (∴ Radius of circle with centre A )
∴ΔOAP is equilateral
⇒∠PAO=60∘
⇒∠BAP=120∘

In ΔBAP, we have
BA=AP and ∠BAP=120∘
:∠ABP=∠APB=30∘
⇒∠PBQ=60∘
Alternate method
Steps of construction
1. Take a point O on the plane of the paper and draw a circle with centre O and radius OA=4 cm.
2. At O construct radii OA and OB such that to ∠AOB equal 120∘ i.e., supplement of the angle between the tangents.
3. Draw perpendicular to OA and OB at A and B, respectively. Suppose these perpendicular intersect at P. Then, PA and PB are required tangents.
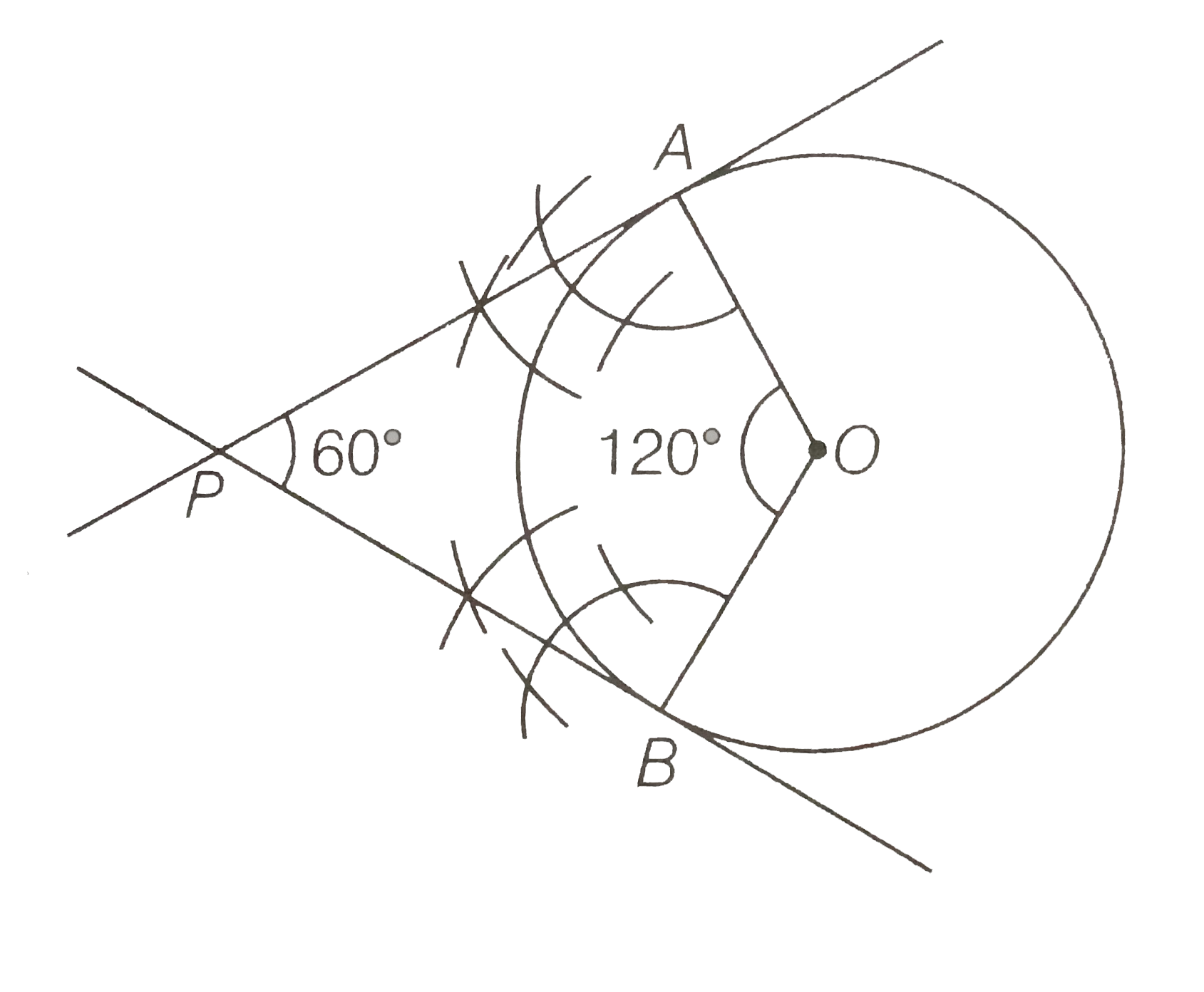
Justification
In quadrilateral OAPB, we have
∠OAP=∠OBP=90∘
and ∠AOB=120∘
∴∠OAP+∠OBP+∠AOB+∠APB=360∘
⇒90∘+90∘+120∘+∠APB=360∘
∴∠APB=360∘−(90∘+90∘+120∘)
=360∘−300∘=60∘
Topper's Solved these Questions
Similar Questions
Draw a circle of radius 4 cm and construct the pair of tangents to the circle from an external point, which is at a distance of 7 cm from its centre.
View SolutionDraw a pair of tangents to a circle of radius 6 cm which are inclined to each other at an angle of 60°. Also justify the construction.
View SolutionWhat is the distance between two parallel tangents of a circle of radius 4 cm?
View SolutionFind the distance between two parallel tangents of a circle of radius 3 cm.
View SolutionDraw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
View SolutionDraw a circle of radius 3.6cm. Draw a tangent to the circle at ant point on it without using the centre.
View SolutionDraw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
View SolutionWhat is the distance between two parallel tangents to a circle of radius 5 cm?
View SolutionDraw a circle with radius 4.2 cm . Construct tangents to the circle from a point at a distance of 7 cm from the centre .
View SolutionDraw a circle with radius 3.2 cm. Construct tangents to the circle from a point at a distance of 6 cm from the centre
View Solution
