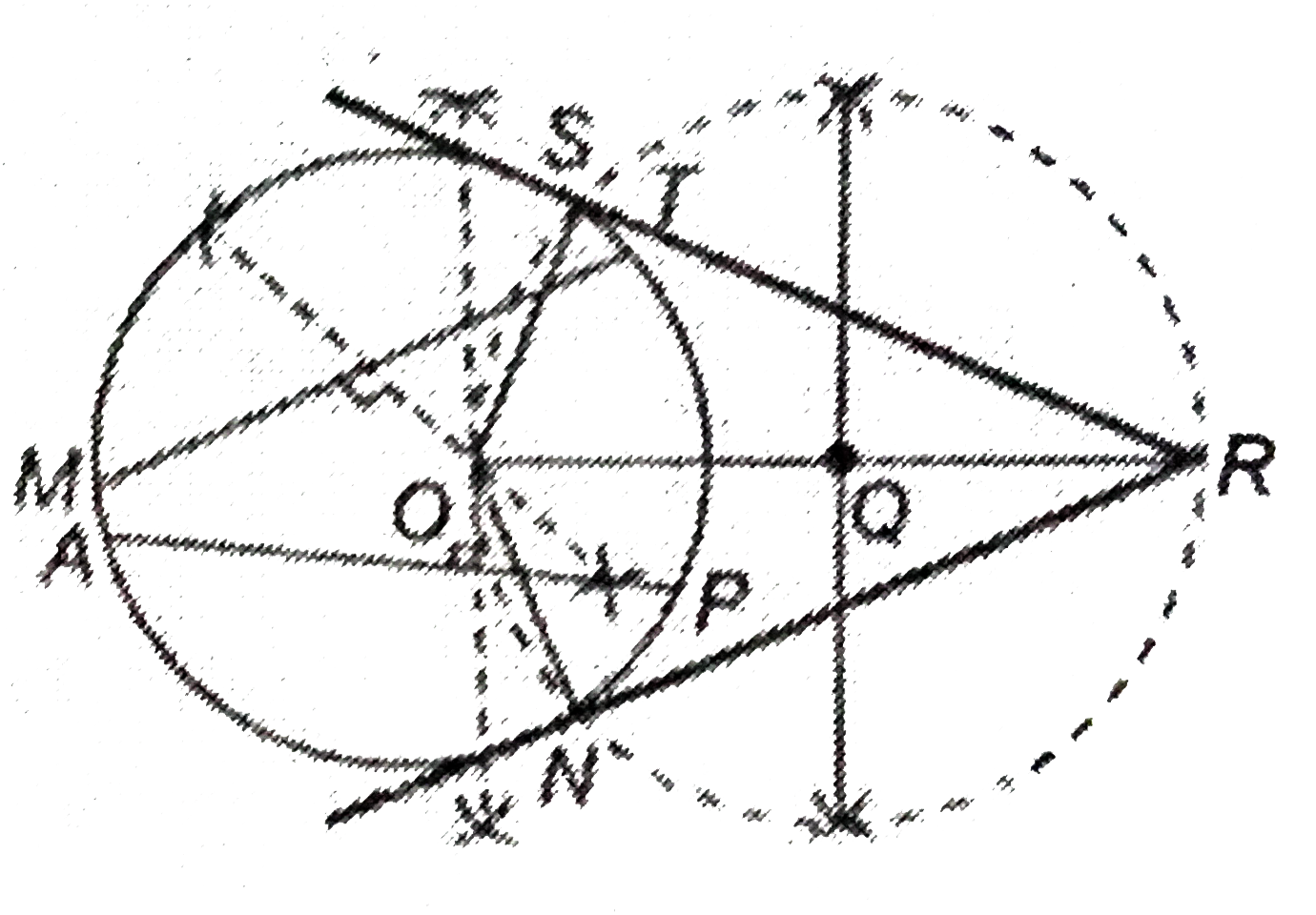
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this points to the circle.
Given, a circle draw by using a bangle and a point R, outside the circle.
Steps of Construction :
1. Draw a circle by using the bangle.
2. Draw two chords Ap and MT. Perpendicular bisectors of AP and MT intersect each other at O which is the centre of the circle.
3. Take a point R outside the circle. Join OR and bisect it.
4. Let Q be the mid-point of OR. Taking Q as centre and OQ as radius draw a dotted circle which intersects the given circle at S and N.
5. Join RS and RN. Thus, RS and RN are the required tangents from R.
Justification : Join OS and ON. Tehn, ∠OSR is the angle lies in the semi-circle, so
∠OSR=90∘
⇒ OS||SR
Since, OS is the radius of the circle with centre O. So, SR has to be a tangent to the circle with centre O. Similarly RN is also a tangent to the circle with centre at O.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - Construction of Tangents to a Circle5videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions5videos
INTRODUCTION TO TRIGONOMETRY
Similar Questions
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
View SolutionDraw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
View SolutionTangents from a Point Outside the circle.
View SolutionDraw a circle of radius 2.5cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle.
View SolutionDraw a circle of radius 2.5cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle.
View SolutionDraw a circle of radius 2.5cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle.
View SolutionDraw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
View SolutionDraw a circle of radius 4 cm. Take a poin P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
View SolutionDraw a circle of radius 4 cm. Take a poin P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
View SolutionDraw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA.
View Solution
