Draw a right angled triangle. Draw the perpendicular bisectors of its sides. Where does the point of concurrency lie?Solution in Marathi
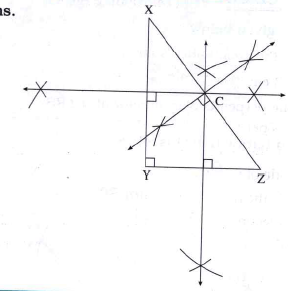
The perpendicular bisectors of the sides of a right angled triangle are concurrent. The point of concurrence C lies at the midpoint of the hypotenuse.
Topper's Solved these Questions
Similar Questions
If 7 kg of onions cost ₹ 140, how much must we pay for 12 kg of onions ?
View SolutionWhich number is neither a prime number nor a composite number?
View SolutionShow that the perpendicular bisectors of the sides of a triangle are concurrent.
View SolutionDraw a triangle whose sides are of lengths 4 cm, 5 cm and 7 cm. Draw the perpendicular bisector of the largest side.
View Solutionरिक्त स्थानों को भरें :
(ii) किसी समकोण त्रिभुज के समकोण वाले शीर्ष से सम्मुख भुजा पर लम्ब खींचने से लम्ब रेखा के दोनों और के त्रिभुज परस्पर ............. होते है ।
View Solution3. Draw an obtuse-angled triangle and a right-angled triangle. Find the points of the concurrence of the angle bisectors of each angle
View SolutionDraw right angled ΔMNP,∠N=90∘, draw perpendicular bisector of MP and angle bisector of ∠N.
View SolutionThe perpendicular bisectors of the sides of a triangle are concurrent.
View SolutionShow that the perpendicular bisectors of the sides of a triangle are concurrent.
View SolutionDraw a right angle and draw its bisector.
View SolutionDraw right angled △MNP,∠N=90∘,draw perpendicular bisector of MP and angle bisector of ∠N.
View SolutionDraw scalene triangle and draw angle bisectors.
View SolutionProve analytically : The perpendicular bisector of the sides of a triangle are concurrent.
View SolutionDraw an obtuse angled triangle and a right angled triangle. Find the point of concurrence of the angle bisectors of each triangle. Where does the point of concurrence lie?
View SolutionWhat is the point of concurrence of the perpendicular bisectors of the sides of a triangle called?
View SolutionDraw an acute angled triangle ABC. Draw all of its altitudes. Name the point of concurrence as O.
View Solution
