Draw a triangle ABC in which BC=4 cm, AB=3 cm and ∠B=450. Also, draw a perpendicular from A on BC.
To construct triangle ABC with the given conditions, follow these steps:
Step-by-Step Construction:
1. Draw Line Segment BC:
- Use a ruler to draw a line segment BC that measures 4 cm.
- Label the endpoints as B and C.
Hint: Ensure that the line is straight and measure accurately using the ruler.
2. Construct Angle B:
- Place a protractor at point B with the baseline along line BC.
- Measure and mark an angle of 45 degrees from line BC.
- Draw a ray from point B through the 45-degree mark. This ray will help locate point A.
Hint: Make sure the protractor is aligned correctly to get an accurate angle.
3. Mark Point A:
- From point B, use a compass to measure a distance of 3 cm (the length of AB).
- With the compass point on B, draw an arc that intersects the ray you just drew. Label the intersection point as A.
Hint: Keep the compass width fixed while drawing the arc to ensure the distance is accurate.
4. Draw Line Segments AB and AC:
- Use a ruler to draw line segments AB and AC, connecting points A to B and A to C.
Hint: Double-check the lengths of AB and AC to ensure they are correct.
5. Draw the Perpendicular from A to BC:
- To draw a perpendicular from point A to line BC, first, place the compass point on A and draw an arc that intersects line BC at two points. Label these points as M and N.
- Without changing the compass width, place the compass point on M and draw an arc above line BC. Then, do the same from point N.
- Label the intersection of these two arcs as point E.
- Finally, draw a line segment AE, which will be the perpendicular from A to line BC.
Hint: Ensure that the arcs from points M and N are of equal radius to accurately find point E.
Final Check:
- Verify that triangle ABC is constructed with the correct lengths and angles.
- Ensure that line segment AE is perpendicular to line BC.
- Use a ruler to draw a line segment BC that measures 4 cm.
- Label the endpoints as B and C.
- Place a protractor at point B with the baseline along line BC.
- Measure and mark an angle of 45 degrees from line BC.
- Draw a ray from point B through the 45-degree mark. This ray will help locate point A.
- From point B, use a compass to measure a distance of 3 cm (the length of AB).
- With the compass point on B, draw an arc that intersects the ray you just drew. Label the intersection point as A.
- Use a ruler to draw line segments AB and AC, connecting points A to B and A to C.
- To draw a perpendicular from point A to line BC, first, place the compass point on A and draw an arc that intersects line BC at two points. Label these points as M and N.
- Without changing the compass width, place the compass point on M and draw an arc above line BC. Then, do the same from point N.
- Label the intersection of these two arcs as point E.
- Finally, draw a line segment AE, which will be the perpendicular from A to line BC.
- Verify that triangle ABC is constructed with the correct lengths and angles.
- Ensure that line segment AE is perpendicular to line BC.
Topper's Solved these Questions
Similar Questions
Draw a triangle ABC in which BC=4 cm, AB=3 cm and ∠B=450. Also, draw a perpendicular from A on BC.
View SolutionDraw a triangle ABC with BC=3.2 cm, AB=3.6 cm and ∠B=1200. Also draw a perpendicular from A on BC .
View SolutionDraw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
View SolutionTriangle ABC is right angled at A.AD is perpendicular to BC. If AB=5 cm, BC=13 cm and AC=12 cm. Find the area of ABC. Also, find the length of AD.
View SolutionDraw a triangle ABC with BC=7cm, ∠B=450and∠C=600. Then construct another triangle, whose sides are 35 times the corresponding sides of triangle ABC.
View SolutionTriangle ABC has AC=13,AB=15 and BC=14. Let Obe the circumcentre of the A B C.Ifthe≤n>hofperpendica––romthep∮'O'onB Ccanbeexpressedasarationalm/n∈thelowestformthenf∈d(m+n).
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionIn which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
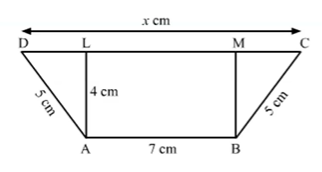 View Solution
View Solution

