Draw angle ABC of any suitable measure.
(i) Draw BP, the bisector of angle ABC.
(ii) Draw BR, the bisector of angle PBC and draw BQ, the bisector of angle ABP.
(iii) Are the angles ABQ, QBP, PBR and RBC equal ?
(iv) are the angles ABR and QBC equal ?
The correct Answer is:(iii) Yes
(iv) Yes.
Step-by-Step Solution:
1. Draw Angle ABC:
- Start by drawing a horizontal line segment BC.
- Choose a point B on this line and draw a semicircle with center B that intersects the line at two points.
- Using a compass, set the width to a suitable measure (for example, 6 cm) and draw an arc from point B that intersects the semicircle.
- Label the intersection point as A.
- The angle ABC is formed by the line segments AB and BC.
Hint: Make sure to keep the compass width consistent when drawing arcs to ensure accuracy.
2. Draw BP, the bisector of angle ABC:
- With the compass still set to the same width, place the compass point at point A and draw an arc that intersects both lines AB and BC.
- Label the intersection points as D and E.
- Now, without changing the compass width, place the compass point at D and draw an arc.
- Repeat this from point E, ensuring the two arcs intersect.
- Label the intersection of the arcs as P.
- Draw a straight line from B through P. This line BP is the bisector of angle ABC.
Hint: The intersection of the arcs from points D and E gives you the point P, which is crucial for accurately bisecting the angle.
3. Draw BR, the bisector of angle PBC:
- Now, we need to bisect angle PBC.
- Place the compass point at point P and draw an arc that intersects lines PB and BC.
- Label the intersection points as F and G.
- Again, without changing the compass width, place the compass point at F and draw an arc.
- Repeat this from point G, ensuring the two arcs intersect.
- Label the intersection of these arcs as R.
- Draw a straight line from B through R. This line BR is the bisector of angle PBC.
Hint: Ensure that the arcs from points F and G intersect clearly to find point R accurately.
4. Draw BQ, the bisector of angle ABP:
- To bisect angle ABP, place the compass point at point A and draw an arc that intersects lines AB and BP.
- Label the intersection points as H and I.
- Place the compass point at H and draw an arc.
- Repeat this from point I, ensuring the two arcs intersect.
- Label the intersection of these arcs as Q.
- Draw a straight line from B through Q. This line BQ is the bisector of angle ABP.
Hint: The angle bisector helps in dividing the angle into two equal parts, so ensure that the arcs intersect properly.
5. Check if angles ABQ, QBP, PBR, and RBC are equal:
- Measure angles ABQ, QBP, PBR, and RBC using a protractor or by reasoning through the construction.
- Since BP, BR, and BQ are angle bisectors, angles ABQ, QBP, PBR, and RBC will all be equal.
Hint: You can use the property of angle bisectors to confirm that the angles are equal.
6. Check if angles ABR and QBC are equal:
- Measure angles ABR and QBC.
- Since ABR is composed of angles ABP and PBR, and QBC is composed of angles QBP and RBC, both should equal 45 degrees.
Hint: Use the sum of angles in a triangle or the properties of angle bisectors to verify the equality.
- Start by drawing a horizontal line segment BC.
- Choose a point B on this line and draw a semicircle with center B that intersects the line at two points.
- Using a compass, set the width to a suitable measure (for example, 6 cm) and draw an arc from point B that intersects the semicircle.
- Label the intersection point as A.
- The angle ABC is formed by the line segments AB and BC.
- With the compass still set to the same width, place the compass point at point A and draw an arc that intersects both lines AB and BC.
- Label the intersection points as D and E.
- Now, without changing the compass width, place the compass point at D and draw an arc.
- Repeat this from point E, ensuring the two arcs intersect.
- Label the intersection of the arcs as P.
- Draw a straight line from B through P. This line BP is the bisector of angle ABC.
- Now, we need to bisect angle PBC.
- Place the compass point at point P and draw an arc that intersects lines PB and BC.
- Label the intersection points as F and G.
- Again, without changing the compass width, place the compass point at F and draw an arc.
- Repeat this from point G, ensuring the two arcs intersect.
- Label the intersection of these arcs as R.
- Draw a straight line from B through R. This line BR is the bisector of angle PBC.
- To bisect angle ABP, place the compass point at point A and draw an arc that intersects lines AB and BP.
- Label the intersection points as H and I.
- Place the compass point at H and draw an arc.
- Repeat this from point I, ensuring the two arcs intersect.
- Label the intersection of these arcs as Q.
- Draw a straight line from B through Q. This line BQ is the bisector of angle ABP.
- Measure angles ABQ, QBP, PBR, and RBC using a protractor or by reasoning through the construction.
- Since BP, BR, and BQ are angle bisectors, angles ABQ, QBP, PBR, and RBC will all be equal.
- Measure angles ABR and QBC.
- Since ABR is composed of angles ABP and PBR, and QBC is composed of angles QBP and RBC, both should equal 45 degrees.
Topper's Solved these Questions
- CONSTRUCTION (USING RULER AND COMPASSES ONLY)BOOK - ICSECHAPTER - CONSTRUCTION (USING RULER AND COMPASSES ONLY)EXERCISE - EXERCISE 18(B)
5 Videos
- CONSTRUCTION (USING RULER AND COMPASSES ONLY)BOOK - ICSECHAPTER - CONSTRUCTION (USING RULER AND COMPASSES ONLY)EXERCISE - EXERCISE 18(C)
6 Videos
- CONSTRUCTION (USING RULER AND COMPASSES ONLY)BOOK - ICSECHAPTER - CONSTRUCTION (USING RULER AND COMPASSES ONLY)EXERCISE - EXERCISE 18(D)
10 Videos
- AREA OF A TRAPEZIUM AND A POLYGONBOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(D)
21 Videos
- CUBES AND CUBE - ROOTS BOOK - ICSECHAPTER - CUBES AND CUBE - ROOTS EXERCISE - EXERCISE 4(B)
39 Videos
Similar Questions
Construct angle ABC=90∘. Draw BP, the bisector of angle ABC. State, the measure of angle PBC.
View SolutionIf the bisector of angle A of the triangle ABC makes an angle θ with BC, then sinθ=
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionDraw an angle ABC of measure 135∘ using a compass.
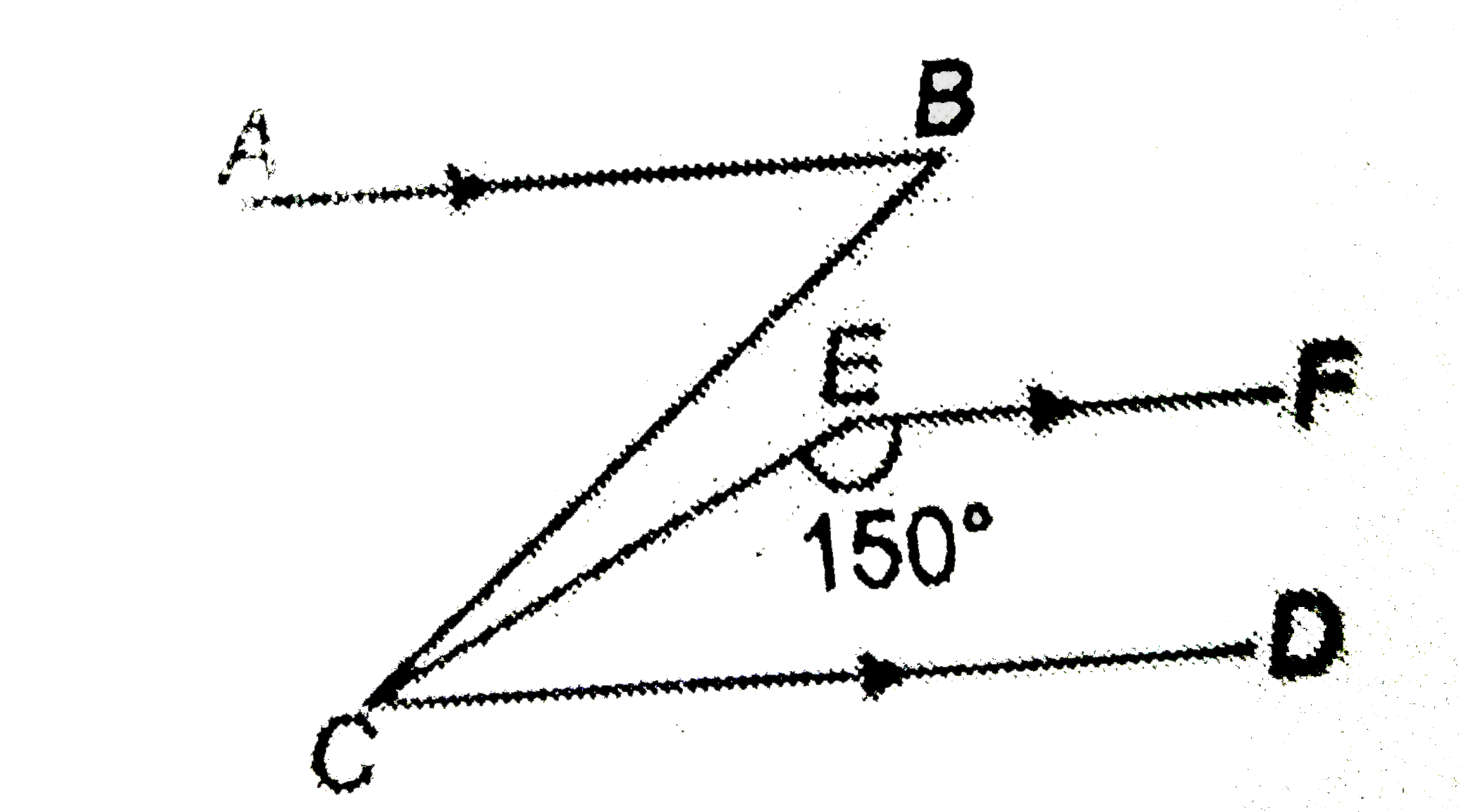
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
View SolutionDraw an angle of 60∘. Draw its bisector.
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View SolutionDraw ∠PQR=75∘ using a protractor.
Draw the angle bisector of ∠PQR using a compass.
View SolutionTriangle ABC is right angles at B. Internet bisectors of acute angles A and C meet at point I. Find the measure of angle AIC
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the relation between angle ACO and angle BCO?
View Solution
