Question

Draw the graph of $f\left(x\right)\text{maximum}\{2\sin x,1-\cos x\},x\in (0,\pi )$. Also find the range of $g\left(x\right)\text{min}\{2\sin x,1-\cos x\},x\in (0,\pi )$

Explanation

Let us first draw graphs of `g_(1)(x) = 2 sin x` and `g_(2)(x) = 1 - cos x`
`g_(1)(0) = g_(1)(pi) = 0, g_(1)(pi//2) = 2`
`g_(2)(x) = sin x gt 0, AA x in (0, pi)`
So `g_(2)' (x)` is increasing.
`g_(2)(0) = 0, g_(2)(pi//2) = 1, g_(2)(pi) = 2`
Graph of functions are as shown in the following figure.

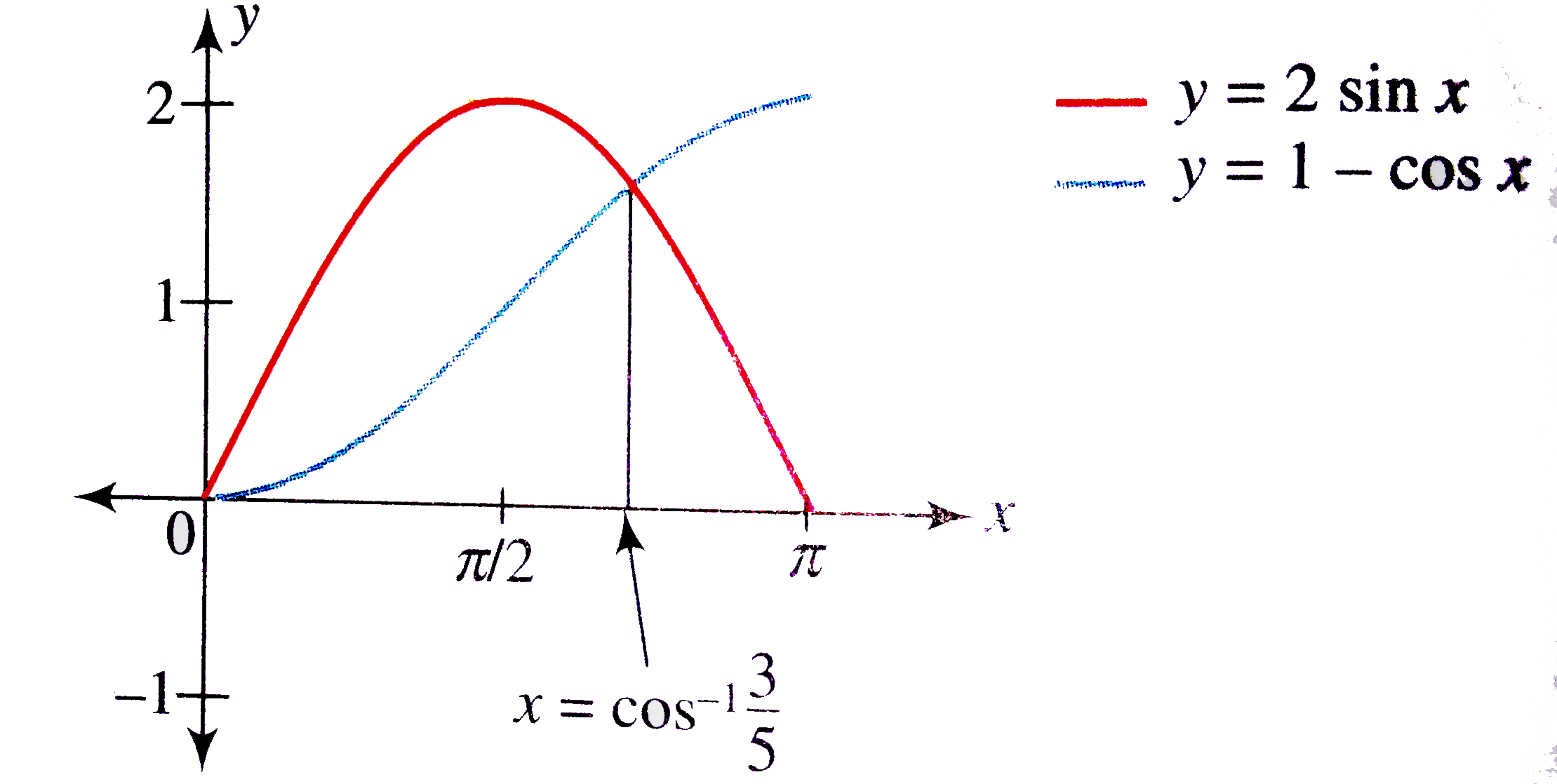
Curves y = 2 sin x and y = 1 - cos x intersect when
`4 sin^(2)x = (1 - cos x)^(2)`
`rArr` `4(1 + cos x) = (1 - cos x)`
`rArr` `4 + 4 cos x = 1 - cos x`
`rArr` `cos x = -3//5`
`rArr` `x = cos^(-1) (-3//5)`
`therefore` `f(x) = {{:(2sinx",", 0 lt x lt pi - "cos"^(-1)(3)/(5)),(1- cos x",", pi - "cos"^(-1)(3)/(5) lt x lt pi):}`
Also the range of `g(x) = min {2 sin x, 1-cosx}` is `[0,1 - cos cos^(-1)(-(3)/(5))] -=[1, 8//5].`