Draw the graph of $f (x) maximum {2 sin x, 1 - cos x}, x \in (0, π)$ . Also find the range of $g (x) min {2 sin x, 1 - cos x}, x \in (0, π)$

Text Solution

Verified by Experts

Let us first draw graphs of $g_{1} (x) = 2 sin x$ and $g_{2} (x) = 1 - cos x$
$g_{1} (0) = g_{1} (π) = 0, g_{1} (π / 2) = 2$
$g_{2} (x) = sin x > 0, \forall x \in (0, π)$
So $g_{2}' (x)$ is increasing.
$g_{2} (0) = 0, g_{2} (π / 2) = 1, g_{2} (π) = 2$
Graph of functions are as shown in the following figure.

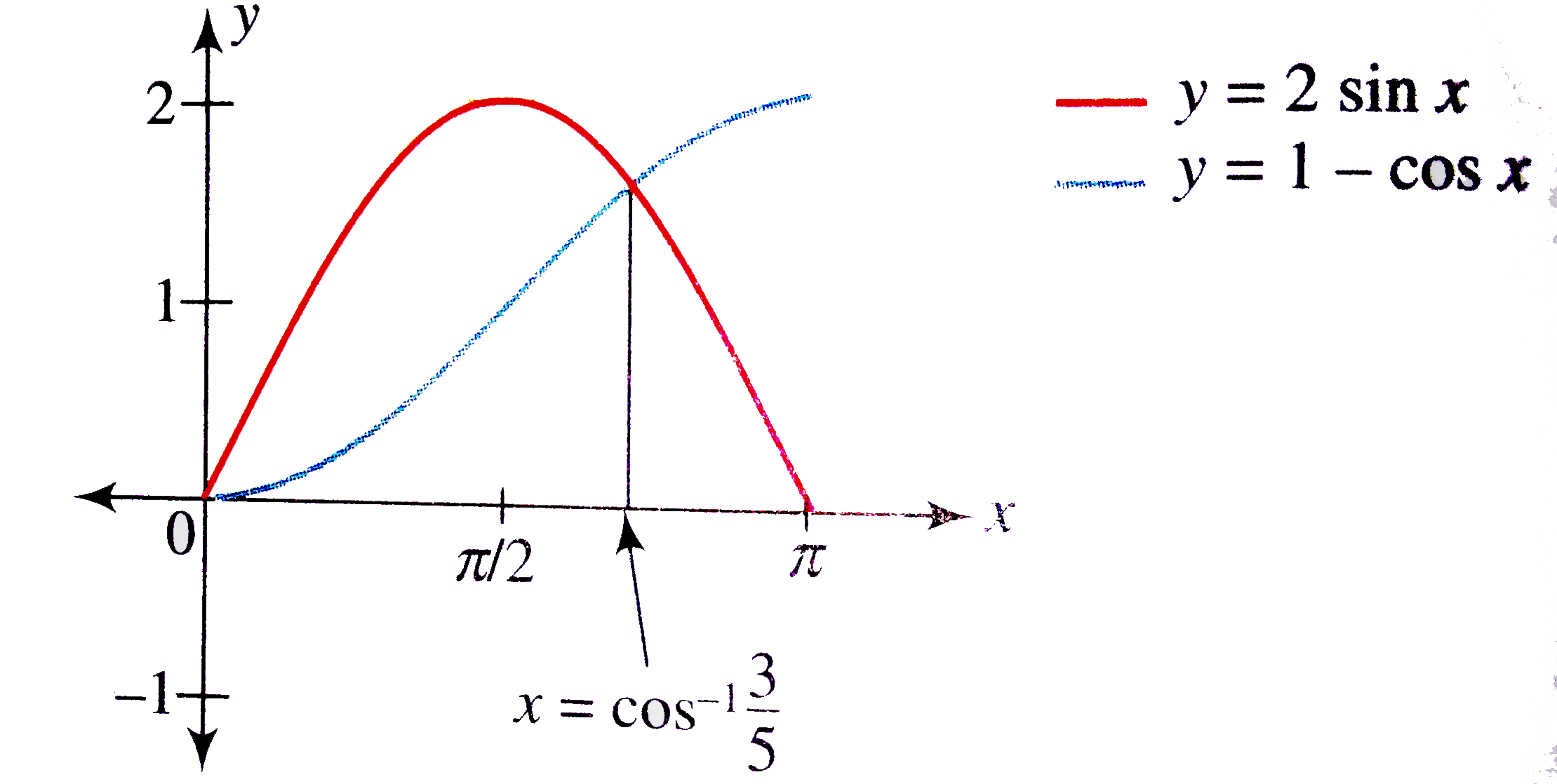
Curves y = 2 sin x and y = 1 - cos x intersect when
$4 {sin}^{2} x = {(1 - cos x)}^{2}$
$\Rightarrow$ $4 (1 + cos x) = (1 - cos x)$
$\Rightarrow$ $4 + 4 cos x = 1 - cos x$
$\Rightarrow$ $cos x = - 3 / 5$
$\Rightarrow$ $x = {cos}^{- 1} (- 3 / 5)$
$∴$ $f (x) = ⎧ ⎨ ⎩ \begin{matrix} 2 sin x, & 0 < x < π - {cos}^{- 1} \frac{3}{5} 1 - cos x, & π - {cos}^{- 1} \frac{3}{5} < x < π \end{matrix}$
Also the range of $g (x) = min {2 sin x, 1 - cos x}$ is $[0, 1 - {cos cos}^{- 1} (- \frac{3}{5})] \equiv [1, 8 / 5] .$

Updated on:21/07/2023

Find the range of $f (x) = {({sin}^{- 1} x)}^{2} + 2 π {cos}^{- 1} x + π^{2}$
A $[\frac{π^{2}}{4}, \frac{9 π^{2}}{4}]$
B $[\frac{3 π^{2}}{4}, \frac{11 π^{2}}{4}]$
C $[\frac{5 π^{2}}{4}, \frac{13 π^{2}}{4}]$
D $[\frac{7 π^{2}}{4}, \frac{15 π^{2}}{4}]$
If $f (x) = 2 x, g (x) = 3 sin x - x cos x, t h e n$ for $x \in (0, \frac{π}{2}) :$
A $f (x) > g (x)$
B $f (x) < g (x)$
C $f (x) = g (x)$ has exactly one real root.
D $f (x) = g (x)$ has exactly two real roots