Draw the graph of $f (x) \sin^{- 1} | \sin x | + \cos^{- 1} (\cos x)$ . Find the range of the function. Find the points of non-differentiability. Also find the value of $\int_{0}^{10 π} [\sin^{- 1} | \sin x | + \cos^{- 1} (\cos x)]$ dxSolution in Bengali

Video Solution

Text Solution

Verified by Experts

$f (x) = {\begin{matrix} \sin^{- 1} (\sin x) + \cos^{- 1} (\cos x) & 0 \leq x < π \\ \sin^{- 1} (\sin x) + \cos^{- 1} (\cos x) & π \leq x \leq 2 π \end{matrix}$
${\begin{matrix} x + x & 0 \leq x < \frac{π}{2} \\ (π - x) + x & \frac{π}{2} \leq x < π \\ - (π - x) + 2 π - x & π \leq x < \frac{3 π}{2} \\ - (x - 2 π) + 2 π - x & \frac{3 π}{2} \leq x \leq 2 π \end{matrix}$
$= {\begin{matrix} 2 x & 0 \leq x < \frac{π}{2} \\ π & \frac{π}{2} \leq x < π \\ π & π \leq x < \frac{3 π}{2} \\ 4 π - 2 x & \frac{3 π}{2} \leq x \leq 2 π \end{matrix}$

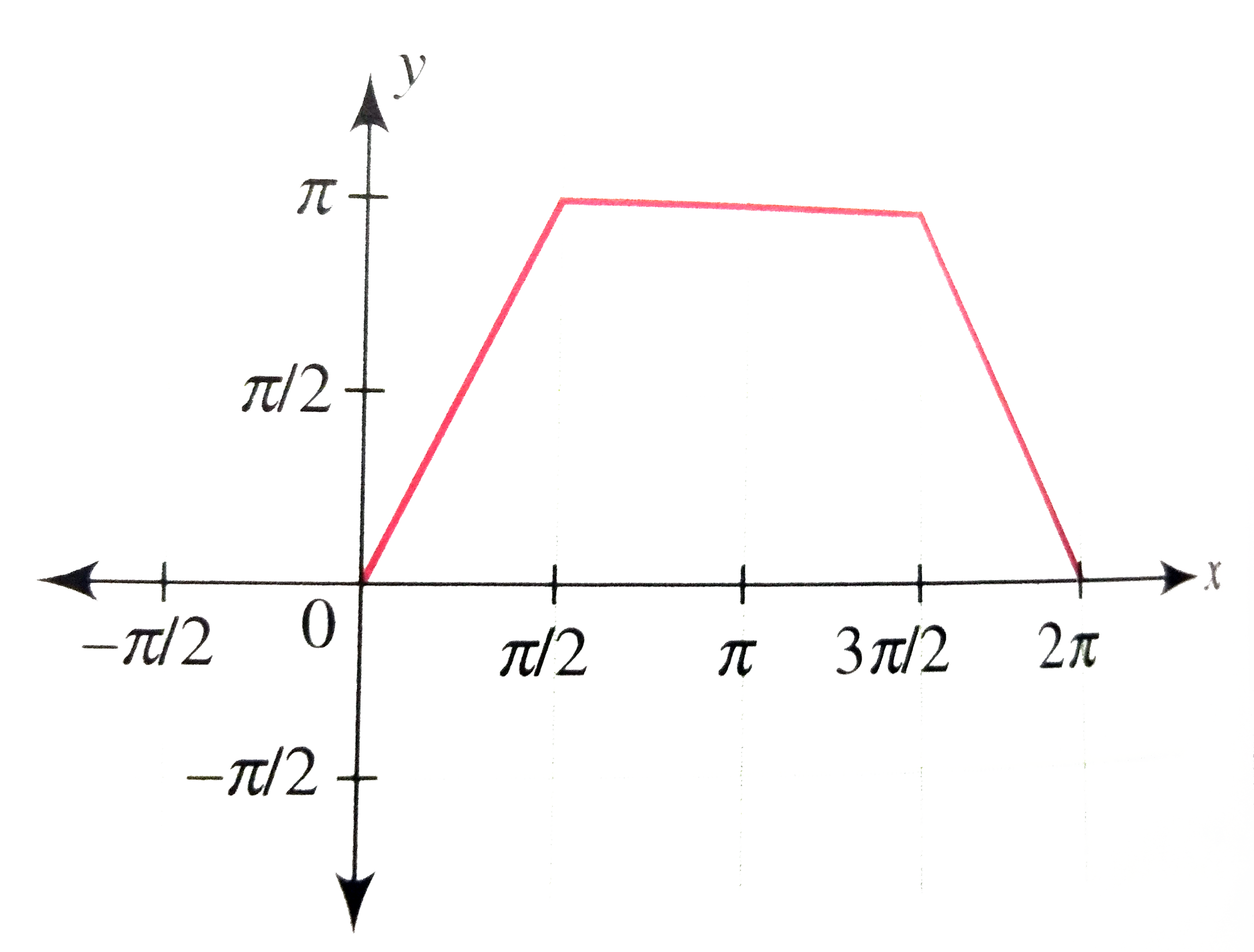
So the graph of the function for $x \in [0, 2 π]$
is as shown inthe adjacent figure.
Now f(x) is a periodic function with period $2 π$ , then the graph of $y = f (x)$ for its domain is as follows.

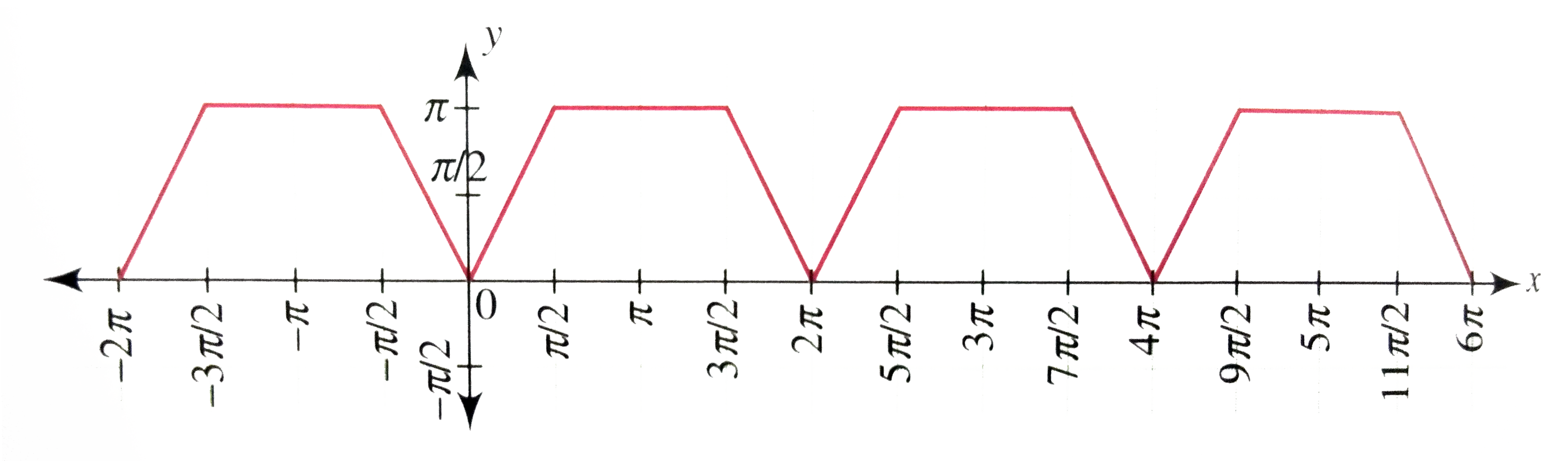
From the graph, the range of the function is $[0, π]$
Function is non-differentiable at $x = 2 n π and x = (2 n + 1) \frac{π}{2}, n \in Z$
$\underset{0}{\int^{10 π}} [\sin^{- 1} | \sin x | + \cos^{- 1} (\cos x)] d x$
$= 5 \times (Area of trapezium formed by the x-axis and the curve in [0, 2 π])$
$= 5 \times (\frac{1}{2} π (2 π + π))$
$= \frac{15 π^{2}}{2}$

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercises

Home
Ask Doubt
Profile