Draw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
To solve the problem of drawing the graph of the solution set for the given inequalities, we will follow these steps:
Step 1: Write down the inequalities
The inequalities given are:
1. 2x+y≥2
2. x−y≤1
3. x+2y≤8
4. x≥0
5. y≥0
Step 2: Convert inequalities to equations
To graph these inequalities, we first convert them into equations:
1. 2x+y=2
2. x−y=1
3. x+2y=8
Step 3: Find intercepts for each equation
For 2x+y=2:
- x-intercept: Set y=0:
2x+0=2⟹x=1(Point: (1, 0))
- y-intercept: Set x=0:
2(0)+y=2⟹y=2(Point: (0, 2))
For x−y=1:
- x-intercept: Set y=0:
x−0=1⟹x=1(Point: (1, 0))
- y-intercept: Set x=0:
0−y=1⟹y=−1(Point: (0, -1))
For x+2y=8:
- x-intercept: Set y=0:
x+2(0)=8⟹x=8(Point: (8, 0))
- y-intercept: Set x=0:
0+2y=8⟹y=4(Point: (0, 4))
Step 4: Graph the lines
Using the intercepts found:
- For 2x+y=2, plot points (1, 0) and (0, 2) and draw a line.
- For x−y=1, plot points (1, 0) and (0, -1) (note that the y-intercept is below the x-axis).
- For x+2y=8, plot points (8, 0) and (0, 4) and draw a line.
Step 5: Determine the shaded regions
- For 2x+y≥2: Shade above the line.
- For x−y≤1: Shade below the line.
- For x+2y≤8: Shade below the line.
- Since x≥0 and y≥0, restrict the shading to the first quadrant.
Step 6: Identify the feasible region
The feasible region is where all shaded areas overlap in the first quadrant. This is the solution set for the inequalities.
Step 7: Mark the vertices of the feasible region
Identify the vertices of the feasible region formed by the intersection of the lines. These points can be found by solving the equations pairwise.
Step 8: Finalize the graph
Draw the final graph, marking the feasible region clearly.
---
The inequalities given are:
1. 2x+y≥2
2. x−y≤1
3. x+2y≤8
4. x≥0
5. y≥0
To graph these inequalities, we first convert them into equations:
1. 2x+y=2
2. x−y=1
3. x+2y=8
For 2x+y=2:
- x-intercept: Set y=0:
2x+0=2⟹x=1(Point: (1, 0))
- y-intercept: Set x=0:
2(0)+y=2⟹y=2(Point: (0, 2))
- x-intercept: Set y=0:
x−0=1⟹x=1(Point: (1, 0))
- y-intercept: Set x=0:
0−y=1⟹y=−1(Point: (0, -1))
- x-intercept: Set y=0:
x+2(0)=8⟹x=8(Point: (8, 0))
- y-intercept: Set x=0:
0+2y=8⟹y=4(Point: (0, 4))
Using the intercepts found:
- For 2x+y=2, plot points (1, 0) and (0, 2) and draw a line.
- For x−y=1, plot points (1, 0) and (0, -1) (note that the y-intercept is below the x-axis).
- For x+2y=8, plot points (8, 0) and (0, 4) and draw a line.
- For 2x+y≥2: Shade above the line.
- For x−y≤1: Shade below the line.
- For x+2y≤8: Shade below the line.
- Since x≥0 and y≥0, restrict the shading to the first quadrant.
The feasible region is where all shaded areas overlap in the first quadrant. This is the solution set for the inequalities.
Identify the vertices of the feasible region formed by the intersection of the lines. These points can be found by solving the equations pairwise.
Draw the final graph, marking the feasible region clearly.
Topper's Solved these Questions
- LINEAR INEQUATIONS (IN TWO VARIABLES )BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN TWO VARIABLES )EXERCISE - EXERCISE 7
22 Videos
- LINEAR INEQUATIONS (IN ONE VARIABLE)BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN ONE VARIABLE)EXERCISE - EXERCISE 6B
12 Videos
- LogarithmBOOK - RS AGGARWALCHAPTER - LogarithmEXERCISE - Exercise 1
9 Videos
Similar Questions
Knowledge Check
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A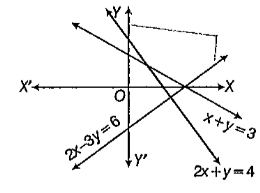 B
B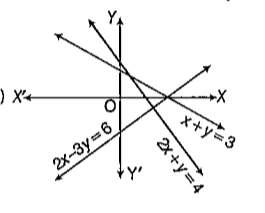 C
C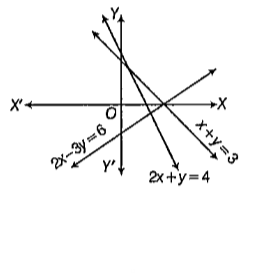 D
D