E is the mid-point of the side BC of the parallelogram ABCD. DE and extended AB intersects each other at F. If AB = 4 cm, then AF = Solution in Bengali
4 cm
8 cm
10 cm
6 cm
The correct Answer is:B
Step by step video, text & image solution for E is the mid-point of the side BC of the parallelogram ABCD. DE and extended AB intersects each other at F. If AB = 4 cm, then AF = by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEOREMS ON TRANSVERSAL AND MID-POINTSBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON TRANSVERSAL AND MID-POINTSEXERCISE - Short answer
10 Videos
- THEOREMS ON TRANSVERSAL AND MID-POINTSBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON TRANSVERSAL AND MID-POINTSEXERCISE - Long answer
14 Videos
- THEOREMS ON TRANSVERSAL AND MID-POINTSBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON TRANSVERSAL AND MID-POINTSEXERCISE - Example-12
1 Videos
- THEOREMS ON CONCURRENCEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON CONCURRENCEEXERCISE - EXERCISE Long-answer type questions
17 Videos
- TRIANGLEBOOK - CALCUTTA BOOK HOUSECHAPTER - TRIANGLEEXERCISE - EXERCISE-1.1 (Long-answer type question :)
14 Videos
Similar Questions
The length of each of the sides of the equilateral triangle ABC is 6 cm. P and Q are the mid-points of AB and AC respectively. Find the length of PQ and the measurement of ∠APQ.
View SolutionProve that the quadrilateral formed by joining the mid-points of the sides of a rectangle is a rhombus, but not a square.
View SolutionA die is thrown once. Find the probability of getting a prime number.
View SolutionFind the value of k for which the given value is a solution of the given equation 7x2+kx−3=0 at x=23
View SolutionThe diagonal of a square is 10√3cm and the area of an equilateral triangle is equal to the area of the square. If a square is constructed on any side of the triangle, then find its area.
View Solutionएक समान्तर चतुभुर्ज ABCD की भुजा BC का मध्य बिन्दु E है। यदि DE व AB को आगे बढ़ने पर ये बिन्दु F पर मिलते है तो AF बराबर होगा :
View SolutionD, E and F are the mid-points of the sides AB, AC and BC of the ΔABC. Prove that DE and AF bisects each other.
View SolutionABCD is a parallelogram in the following figure. The midpoint of BC is E. Prove that AB and DE are AF = 2AB, extended to F.
View SolutionIn the given figure ABCD is a parallelogram and E is the midpoint of BC. If DE and AB are further extended to meet point F then prove that AF = 2AB.
View SolutionIn the adjacent figure ABCD is a parallelogram and E is the midpoint of the side BC. If DE and AB are produced to meet at F, show that AF=2AB.
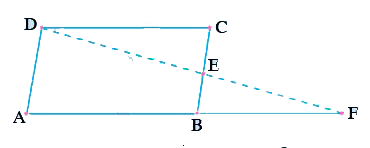
View SolutionIn the adjacent figure ABCD is a parallelogram and E is the midpoint of the side BC. If DE and AB are produced to meet at F, show that AF=2AB.
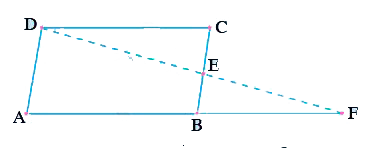
View SolutionIn the adjacent figure ABCD is a parallelogram and E is the midpoint of the side BC. If DE and AB are produced to meet at F, show that AF=2AB.
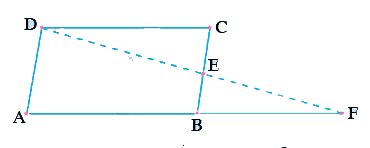
View SolutionIn the adjacent figure ABCD is a parallelogram and E is the midpoint of the side BC. If DE and AB are produced to meet at F, show that AF=2AB.
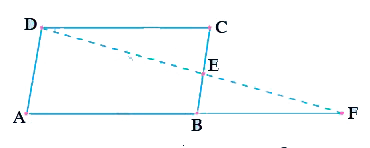
View SolutionIn Fig. . ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB, when produced meet at F, prove that AF = 2AB.
View SolutionIn the figure, ABCD is a parallelogram and E is the midpoint of the side BC. When DE and AB are extended, they meet at point F. Prove that AF = 2 AB
View Solution
