In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
To prove that in trapezium ABCD, where AB and DC are parallel, and E is the midpoint of AD and F is the midpoint of BC, the equation AB+DC=2EF holds, we can follow these steps:
1. Draw the trapezium ABCD:
- Let AB and DC be the parallel sides.
- Mark E as the midpoint of side AD and F as the midpoint of side BC.
2. Label the points:
- Let G be the midpoint of line segment AI, H be the midpoint of line segment BJ, I be the midpoint of line segment CJ, and J be the midpoint of line segment DI.
3. Apply the Midpoint Theorem:
- According to the Midpoint Theorem, if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half its length.
- In triangle ADI, since E and G are midpoints, we have:
EG=12DI
- In triangle BJC, since F and H are midpoints, we have:
HF=12JC
4. Express AB and DC in terms of EF:
- From the trapezium, we can express the lengths of AB and DC:
AB=IJ=GH(since AB∥DC)
DC=CJ+IJ+ID=CJ+AB+EG
- Substitute the values of CJ and ID using the Midpoint Theorem:
CJ=2HFandID=2EG
- Therefore, we can rewrite DC as:
DC=2HF+AB+2EG
5. Combine the expressions:
- Now, we can add AB and DC:
AB+DC=AB+(2HF+AB+2EG)
=2AB+2HF+2EG
- Factor out the 2:
=2(AB+HF+EG)
6. Relate to EF:
- Notice that EF=GH+HF+EG (since GH, HF, and EG are segments forming EF).
- Therefore, we can substitute:
AB+DC=2EF
7. Conclusion:
- We have shown that AB+DC=2EF, thus proving the statement.
- Let AB and DC be the parallel sides.
- Mark E as the midpoint of side AD and F as the midpoint of side BC.
- Let G be the midpoint of line segment AI, H be the midpoint of line segment BJ, I be the midpoint of line segment CJ, and J be the midpoint of line segment DI.
- According to the Midpoint Theorem, if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half its length.
- In triangle ADI, since E and G are midpoints, we have:
EG=12DI
- In triangle BJC, since F and H are midpoints, we have:
HF=12JC
- From the trapezium, we can express the lengths of AB and DC:
AB=IJ=GH(since AB∥DC)
DC=CJ+IJ+ID=CJ+AB+EG
- Substitute the values of CJ and ID using the Midpoint Theorem:
CJ=2HFandID=2EG
- Therefore, we can rewrite DC as:
DC=2HF+AB+2EG
- Now, we can add AB and DC:
AB+DC=AB+(2HF+AB+2EG)
=2AB+2HF+2EG
- Factor out the 2:
=2(AB+HF+EG)
- Notice that EF=GH+HF+EG (since GH, HF, and EG are segments forming EF).
- Therefore, we can substitute:
AB+DC=2EF
- We have shown that AB+DC=2EF, thus proving the statement.
Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(A)
23 Videos
- MENSURATION (PLANE FIGURE) BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-3 (4 Marks Questions)
8 Videos
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
Similar Questions
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
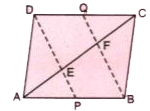
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that AE=EF=FC.
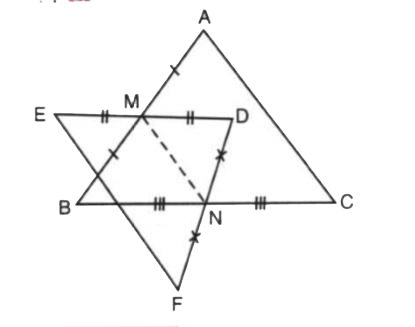
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
View SolutionIn trapezium ABCD, AB//DC. M is mid point of AD and N is mid-point of BC.
If AB = 8 cm and DC = 11 cm , find MN.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.
View Solution
