Each coefficient in equation ax2+bx+c=0 is obtained by throwing an ordinary die. Find the probability that the equation has real roots.Solution in Tamil
The correct Answer is:P(A)=43216
Step by step video, text & image solution for Each coefficient in equation ax^(2) + bx + c = 0 is obtained by throwing an ordinary die. Find the probability that the equation has real roots. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Statistics
4 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Similarity
9 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Financial planning
6 Videos
- ARITHMETIC PROGRESSION BOOK - CHETAN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - ASSIGENMENT -3
10 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
Similar Questions
The mean of the following frequency distribution is 50. Find the value of f:
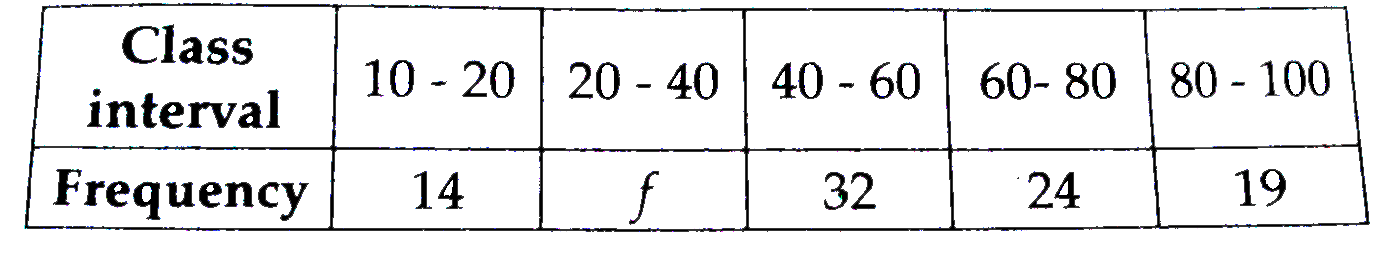
View SolutionBisector of ∠B and ∠C in ΔABC meet each other at P. Line Ap cuts the side BC at Q. Then prove that : APPQ=AB+BCBC

View SolutionMr. Modi invested Rs. 30,120 in equity shares of FV Rs. 10 when the market value was Rs. 60. After receiving dividend on them at 90%, he sold them at MV of Rs.55. In each transaction he paid 0.4% brokerage. What was the total gain or loss in this transaction ?
View SolutionWhat is the common difference (d) of the A.P. 2,-2,-6,-10….. ?
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.

View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary six faced die. Find the probability that the equation will have real roots.
View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary six faced die. Find the probability that the equation will have real roots.
View SolutionEach coefficient in the equation ax2+bx+c=0 is obtained by rolling a die. Find the probability that the equation has equal roots.
View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary die.
Q. The probability that roots of quadratic are real and distinct, is
View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary die.
Q. The probability that roots of quadratics are real and district, is
View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary die.
Q. The probability that roots of quadratic are imaginary, is
View SolutionIf a sum of money double itself in 4 years at S.I. then the rate of interest per annum is?
View SolutionThe coefficients b and c of the equation x2+bx+c=0 are determined by throwing an ordinary die. The probability that the equation has equal roots is
View SolutionEach coefficient in the equation ax2+bx+c=0 is determined by throwing an ordinary six faced die. Find the probability that the equation will have real roots.
View SolutionThe coefficients a, b and c of the quadratic equation, ax2+bx+c=0 are obtained by throwing a dice three times. The probability that this equation has equal roots is:
View Solution
