Bisector of ∠B and ∠C in ΔABC meet each other at P. Line Ap cuts the side BC at Q. Then prove that : APPQ=AB+BCBC
 Solution in Tamil
Solution in Tamil
The correct Answer is:∴APPQ=AB+ACBC
Step by step video & image solution for Bisector of angleB" and "angle C " in "DeltaABC meet each other at P. Line Ap cuts the side BC at Q. Then prove that : (AP)/(PQ)=(AB+BC)/(BC) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Theorem of Pythagoras7videos
CHALLENGING QUESTIONS
- BOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Circle9videos
CHALLENGING QUESTIONS
- BOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Statistics4videos
CHALLENGING QUESTIONS
- BOOK - CHETAN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - ASSIGENMENT -310videos
ARITHMETIC PROGRESSION
- BOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):3videos
CIRCLE
Similar Questions
In ΔPQR,∠PQR=90∘, as show in figure, seg QS⊥sPR, seg QM is angle bisector of ∠PQR.
Prove that : PM2MR2=PSSR
 01:37View Solution
01:37View SolutionFrom the end points of a diameter a diameter of circle perpendiculars are drawn to a tngent of the same circle. Show their feet on the tangent are equidistant from the centre of the circle.
02:11View SolutionThe mean of the following frequency distribution is 50. Find the value of f:
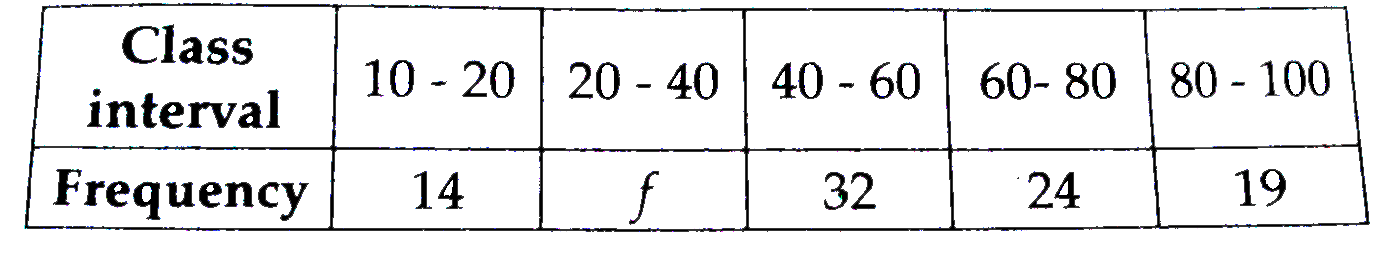 01:31View Solution
01:31View SolutionWhat is the common difference (d) of the A.P. 2,-2,-6,-10….. ?
02:46View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.
 04:23View Solution
04:23View SolutionHow many lines of symmetry does the above figure have ?
01:28View SolutionDetermine the point of symmetry of a regular hexagon.
02:45View SolutionDtermine the images of the following figure about the given line :
02:17View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
05:41View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt02:10View SolutionDraw the bisector of ∠AOB=58∘
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VII_C05_S01_009_Q01.png" width="80%"gt02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 01:59View Solution
01:59View SolutionMatch the following Column A to Column B
 01:19View Solution
01:19View SolutionThe inequation represented by the graph given below is :
02:02View Solution

