Equation(s) of the straight line(s), inclined at 300 to the x-axis such that the length of its (each of their) line segment(s) between the coordinate axes is 10 units, is (are) (a) x+√3y+5√3=0 (b)x−√3y+5√3=0 (c)x+√3y−5√3=0 (d)x−√3y−5√3=0Solution in Tamil
x+√3y+5√3=0
x−√3y+5√3=0
x+√3y−5√3=0
x−√3y−5√3=0
The correct Answer is:B, D
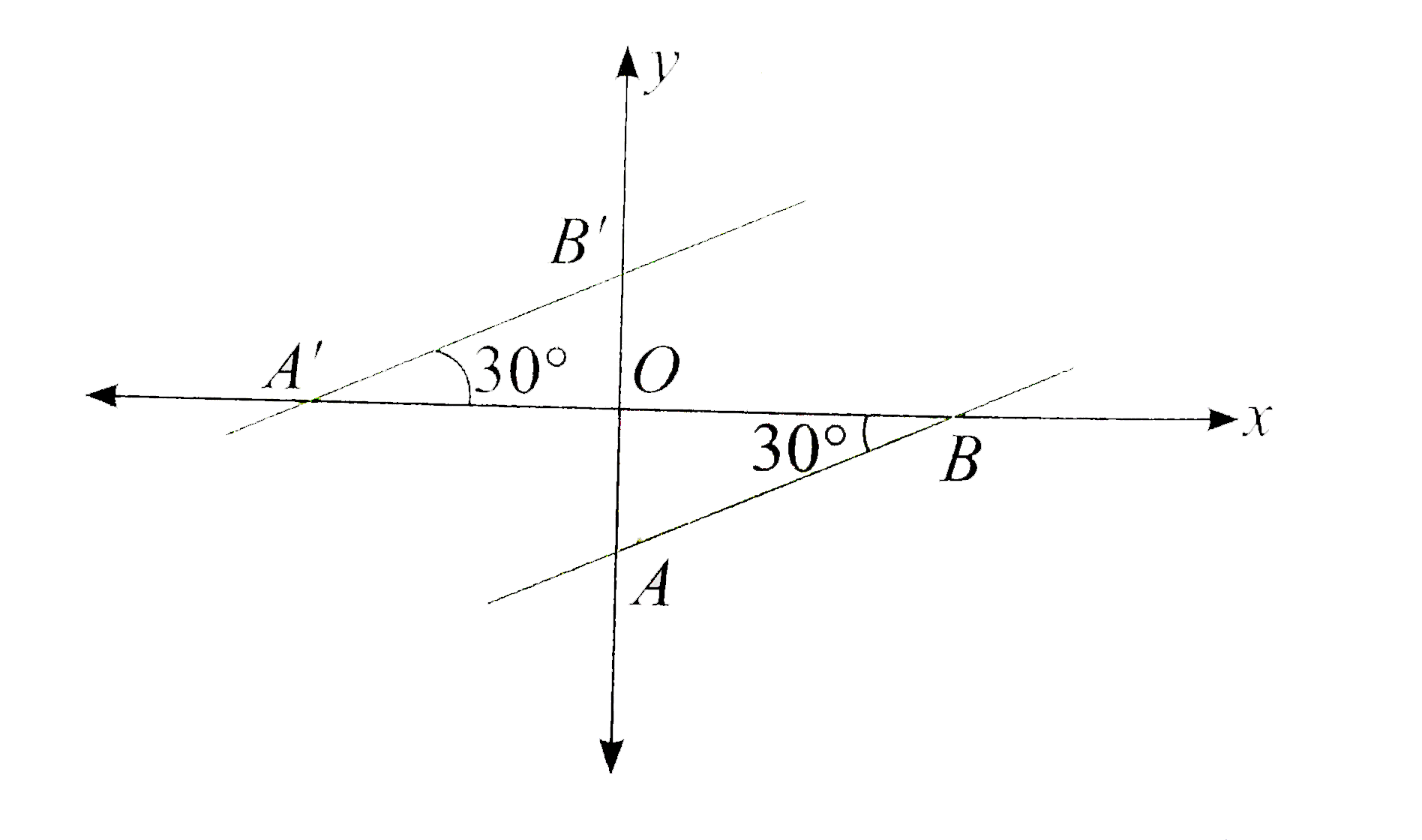
According to the question, AB=10. So, OA=10 sin30∘=5. Then the equation of line is
y=1√3x±5
or x−√3y±5√3=0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)8videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)82videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Let L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is03:08View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:
 03:37View Solution
03:37View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
01:46View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:33View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
02:04View SolutionFind the angle between the lines y−√3x−5=0and √3y−x+6=0.
03:24View SolutionEquation(s) of the straight line(s), inclined at 300 to the x-axis such that the length of its (each of their) line segment(s) between the coordinate axes is 10 units, is (are) x+√3y+5√3=0 x−√3y+5√3=0 x+√3y−5√3=0 x−√3y−5√3=0
02:42View SolutionThe inclination of the line sqrt(3)x-y+5=0 with x -axis is
05:13View SolutionFind the angles between the pairs of straight lines: x+√3y−5=0 and √3x+y−7=0
04:01View SolutionThe angle between the lines √3x−y−2=0andx−√3y+1=0 is
02:47View Solutionरेखाओं y−√3x−5=0 तथा √3y−x+6=0 के बीच का कोण निकालें।
02:47View SolutionFind the angle between the lines y−√3x−5=0and√3y−x+6=0
06:45View Solutiony−√3x−5=0 और √3y−x+6=0 रेखाओं के बीच का कोण ज्ञात कीजिए |
04:34View SolutionFind the angle between the lines y−√3x−5=0and √3y−x+6=0.
04:02View SolutionEquation(s) of the straight line(s), inclined at 30∘ to the x-axis such that the length of its (each of their) line segment(s) between the coordinates axes is 10 units, is (are)
04:58View SolutionEquation(s) of the straight line(s), inclined at 300 to the x-axis such that the length of its (each of their) line segment(s) between the coordinate axes is 10 units, is (are) x+√3y+5√3=0 x−√3y+5√3=0 x+√3y−5√3=0 x−√3y−5√3=0
05:05View Solution

