The point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
α=−1
α=−12
α=12
−67<α<32
The correct Answer is:B, C, D
We have A(0,3),B(−2,0) and C(6,1)
Equation of AC is x+3y−9=0
Equation of BC is x−8y+2=0
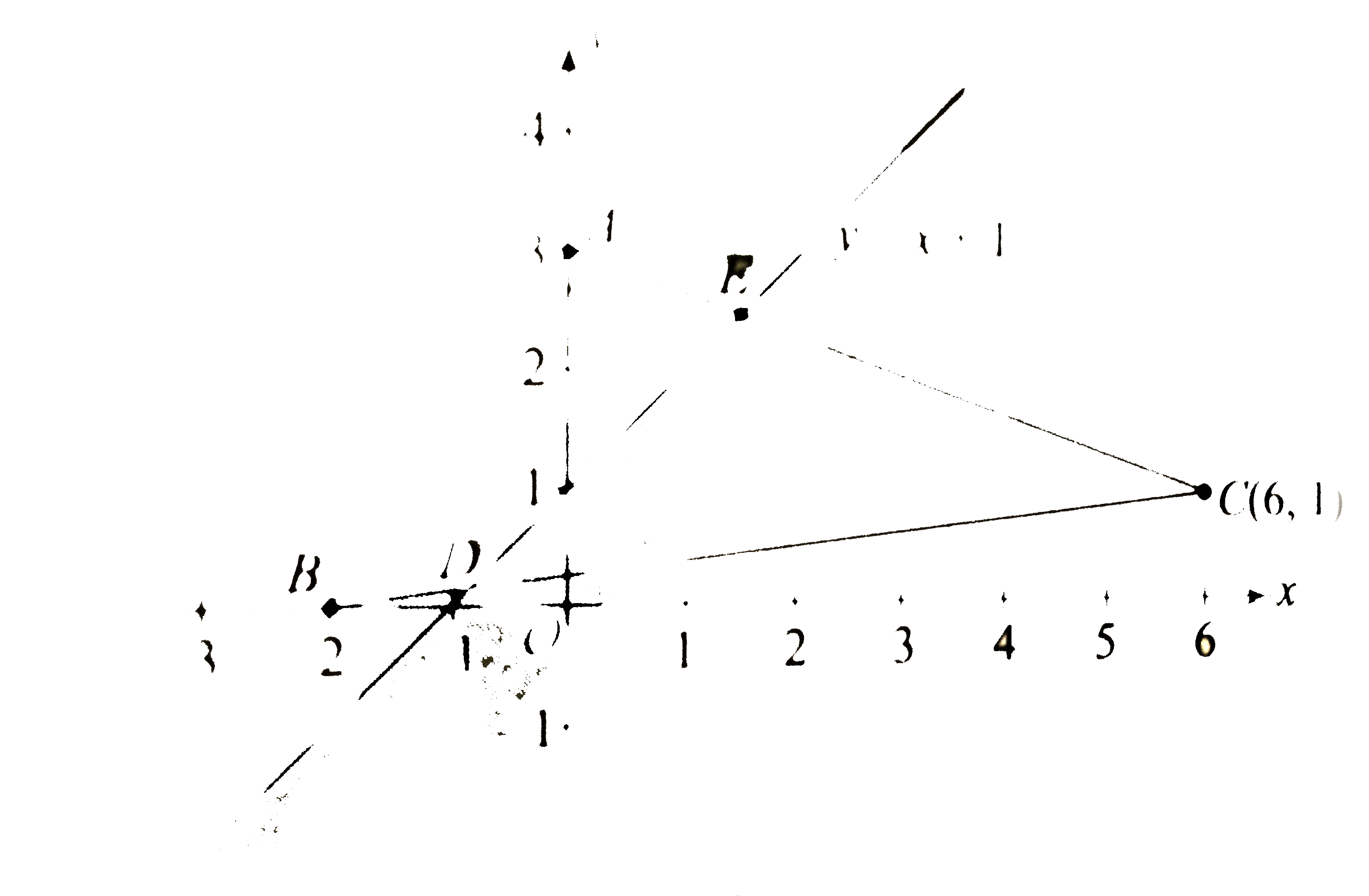
P(α,α+1) lies on the line y=x+1
whichcuts BC at D(−67,17) and AC at E(32,52)
∴α must lie between −67and 32.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area of the triangle whose vertices are A(1,2−1) B (3,1,4) and C (0,2,3)
A√1762sp unitB8 sq unitC√1862 sq unitDNone of these
Find the value of alpha for which the P(2+cosα,sinα) lies inside the triangle having vertices (2,0),(−7,0)and(−1,√3).
View SolutionFind the area of the triangle formed by joining the mid -points of the sides of the triangle ABC ,whose vertices are A(0,-1),B(2,1)andC(0,3).
View SolutionFind the values of α such that the variable point (α,tanα) lies inside the triangle whose sides are
y=x+√3−π3,x+y+1√3+π6=0 and x−π2=0
View SolutionFind the values of α such that the variable point (α,tanα) lies inside the triangle whose sides are
y=x+√3−π3,x+y+1√3+π6=0 and x−π2=0
View SolutionFind the values of α so that the point P(α2,α) lies inside or on the triangle formed by the lines x−5y+6=0,x−3+2=0andx−2y−3=0.
View SolutionFind the values of α so that the point P(α2,α) lies inside or on the triangle formed by the lines x−5y+6=0,x−3y+2=0 and x−2y−3=0.
View SolutionIf point P(α,α2−2) lies inside the triangle formed by the lines x+y=1,y=x+1andy=−1 then α∈
View Solution
