Etiennne is graphing the quadratic equation y=x2−8x−48. He substtitute 0 for x and finds that the y-intercept of the graph is-48. Next, he wants to plot the x-intercepts of the graph, so he rewrites the equation in a different form. Assuming he rewrote the equations correctly and the equation reveals the x-intercepts, which of the following Etienne's new equations?
Y=(x−8)2−16
y=(x−8)2+16
y=(x−8)(x+6)
y=(x−12)(x+4)
The correct Answer is:D
To solve the problem, we need to rewrite the quadratic equation y=x2−8x−48 in a form that reveals the x-intercepts. Here’s how we can do it step by step:
Step 1: Set the equation to find x-intercepts
To find the x-intercepts, we set y=0:
0=x2−8x−48
Step 2: Rearrange the equation
This gives us the quadratic equation:
x2−8x−48=0
Step 3: Factor the quadratic equation
Next, we need to factor the quadratic expression. We are looking for two numbers that multiply to −48 (the constant term) and add to −8 (the coefficient of x). The numbers that satisfy this are −12 and 4.
So we can rewrite the equation:
x2−12x+4x−48=0
Step 4: Group the terms
Now, we can group the terms:
(x2−12x)+(4x−48)=0
Step 5: Factor by grouping
Factoring out the common terms from each group:
x(x−12)+4(x−12)=0
Now we can factor out (x−12):
(x−12)(x+4)=0
Step 6: Solve for x-intercepts
Setting each factor to zero gives us the x-intercepts:
x−12=0⇒x=12
x+4=0⇒x=−4
Thus, the x-intercepts are (12,0) and (−4,0).
Final Answer
Etienne's new equation that reveals the x-intercepts is:
(x−12)(x+4)=0
To find the x-intercepts, we set y=0:
0=x2−8x−48
This gives us the quadratic equation:
x2−8x−48=0
Next, we need to factor the quadratic expression. We are looking for two numbers that multiply to −48 (the constant term) and add to −8 (the coefficient of x). The numbers that satisfy this are −12 and 4.
x2−12x+4x−48=0
Now, we can group the terms:
(x2−12x)+(4x−48)=0
Factoring out the common terms from each group:
x(x−12)+4(x−12)=0
(x−12)(x+4)=0
Setting each factor to zero gives us the x-intercepts:
x−12=0⇒x=12
x+4=0⇒x=−4
Etienne's new equation that reveals the x-intercepts is:
(x−12)(x+4)=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the y- intercept of the line by the equation 7x−3y=21?
A−7B−73C73D7The graph of the equation y=x3+5x+1
ADoes not intersect the x-axisBintersects the x-axis at one and only one pointCintersects the x-axis at exactly three pointsDintersects the x-axis at more than three points.If the graph of the equation y=5x+3 is shifted down 4 units, what is the x-intercept of the new line?
A−1B15C1D54
Draw the graph of the equation 2x+y=3
View Solution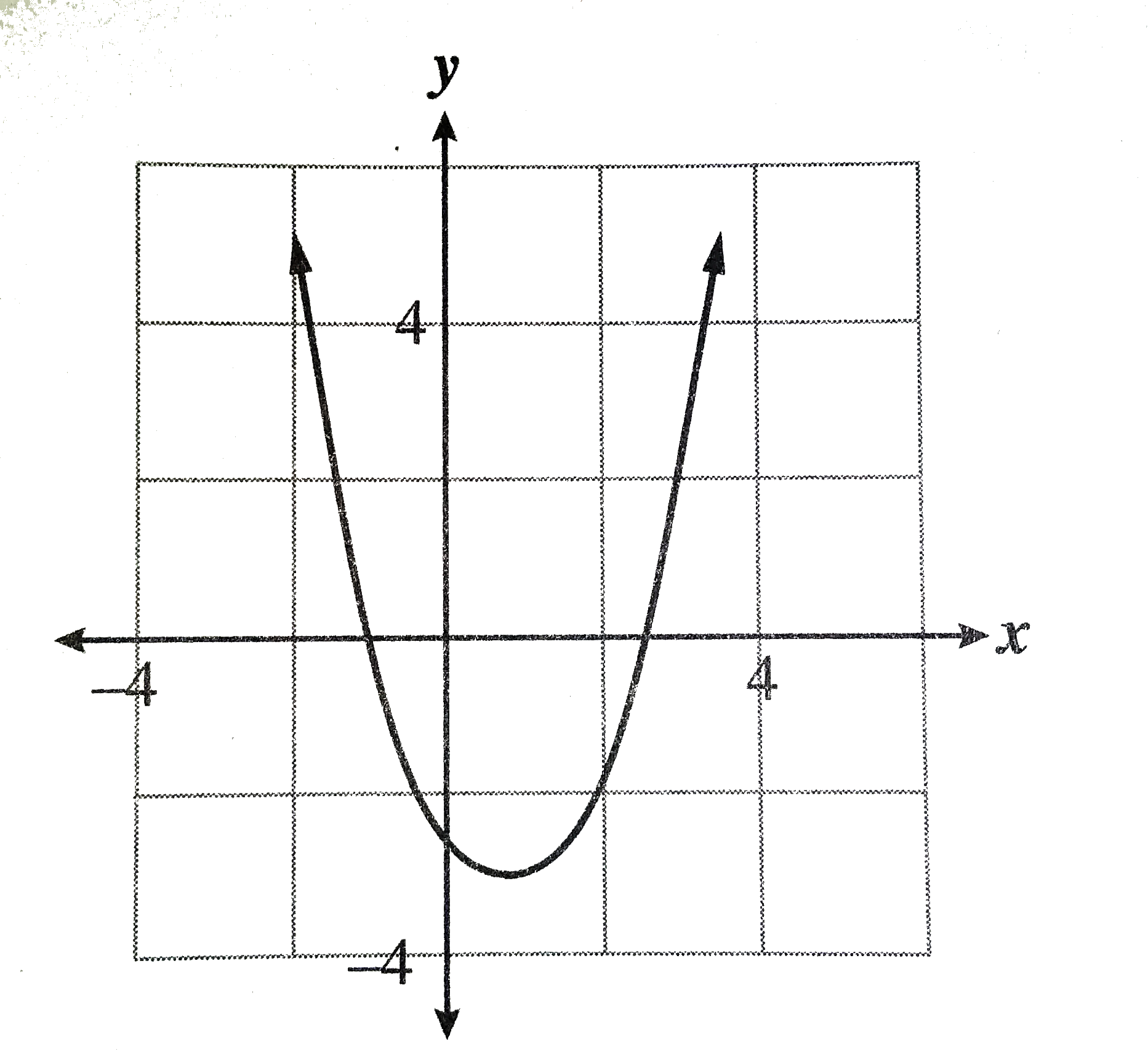
Each of the following quadratic equations represents the graph shown above. Which equation reveals the exact values of the x-intercepts of the graph?
View SolutionReduce the equations to the intercept form 2x−3y=5
View SolutionReduce the equations to the intercept form 4x−3y=6
View SolutionDraw the graph of the equation x−y=0.
View Solution
