Question

Euclid Division lemma

Explanation

Euclid Division lemma

Let us begin with a famous problem/riddle:

A trader was on his way to sell eggs where he met an idler. As the idler did not have any work to do, so he started arguing with the trader. The situation got so tensed that it led to a fight where the idler pulled the egg basket, and it dashed on the floor, thereby breaking the eggs. After this, the trader contacted the Panchayat where he was asked as to how many eggs were broken. The trader provided the following responses:

• If counted in threes, two will remain;


• If counted in fives, four will remain;


• If counted in sevens, nothing will remain;


• If counted in sixes, five will remain;


• If counted in pairs, one will remain;


• If counted in fours, three will remain;


• My basket cannot hold more than 150 eggs.

Well, the main task is to find the number of eggs in the basket. This proves to be a good example of how to obtain a quotient and remainder. We will have a look at the solution of this problem step by step.

Suppose x is the number of eggs.

It is to be noted that x should be the multiple of 7, so we find:

x = 7a, a ∈Z

If we count in pairs, then one egg remains, i.e.

x = 2b +1, b ∈ Z

We can say that x is odd.

Now, we will find out all the odd multiples of 7 and less than 150

Here it goes:  7, 21, 35,  49,  63,  77, 91,  105,  119,  133,  147

It is to be noted that x cannot be multiplied by 3 or 5. So, we will delete all the multiples of 3 or 5 where we get:

7,  21,  35,  49,  63,  77, 91,  105,  119,  133,  147

So, now we have six possible numbers with us which are 7,49,77,91,119,133

Then it has been mentioned that three will remain if it is counted in fours, so

X needs to be one less than a multiple of 4. Now, if we delete the numbers that are not less than a multiple of 4, we get:

7, 49,  77,  91,  119,  133.

Also, x must be one less than a multiple of 3 where it also must be one less than a multiple of 5. Here, we get:

7,  91,  119

So, we can conclude by saying that 119 eggs were present in the basket.

We can verify this as:

      2 (59) + 1

      3 (39) + 2

      4 (29) + 3

      5 (23) + 4

      6 (19) + 5

      7 (17) + 0

So, the above data sums to 119.

Related Videos:

• Proof of Euclid division lemma


• What is Euclid Division ?


• Euclid division algorithm

What is Euclid’s Division Lemma?

According to Euclid’s Division Lemma if there is a given two positive integers a and b, then there exist unique integers q and r such that:

a=bq+r,0⩽r<b

The integer q happens to be quotient where the remainder is the integer r. Here the quotient and remainder are unique. In simple words, if an integer is divided by a non-zero integer, a unique quotient integer would be derived along with a unique remainder integer.

Let’s have some look at the examples regarding the application of this lemma:

17 = 3 (5) + 2

24 = 7 (3) + 3

61 = 11 (5) + 6

 7 = 12 (0) + 7

You have seen that there are some underlined numbers which are dividend and divisor. Regarding the numbers that are in brackets, they are quotient.  Regarding the last number, it is the remainder.

A visual model for Euclid’s Division Lemma

Let’s take an arbitrary integer, say 37 now, if you need to divide this by 7 then what would be the remainder and quotient.

Here, we will get:

37=7(5)+2

So, we can find that the quotient is 5 and the remainder is 2.

In order to interpret this physically, we need to divide the number line into blocks of 7 units. Have a look at the below figure.

In the figure, you have seen that each block has been named.  Can you tell as to which block will 37 lie?  Well, you need to get the right understanding that it would lie in B5.  As you can see that there are 5 intervening blocks from B0 to B4. Therefore, it corresponds to the quotient.

Now, can you find the interpretation of the remainder? Well, for this, you need to zoom-in block B5. So, it will be 7 units long:

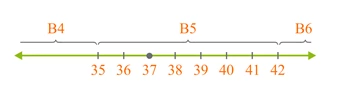
Cleary, 37 lies 2 units from the start of its block (which is B5). This corresponds to the remainder.

Let us get this process repeat again. If we need to divide 80 by 9 then here we have to divide the number line into blocks of 9 units each. It will be in block B8 that the number 80 will lie which is 8 units from the start of its block:

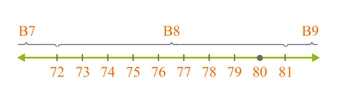
Thus we can find that the quotient is 8, whee 8 happen to be the remainder.

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 10 Chapter Real Number